��Ŀ����
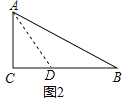
����Ŀ�����壺�������������һ��������߶ΰ���������ηֳ�����С�����Σ�����һ���������ǵ��������Σ�����һ�������κ�ԭ�����ε������ڽǷֱ���ȣ���ô�����߶γ�Ϊԭ�����ε�����г�ָ����������磺��ͼ1������ֱ��������б���ϵ����߾���һ������г�ָ�����.
��1���жϣ��ԵĴ����̡������Ĵ���������
�ٵȱ������δ�������г�ָ��������� ����
���������������һ��������һ���ǵ�����������������αش�������г�ָ��������� ����
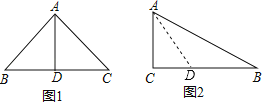
��2����ͼ2��Rt��ABC����C��90������B��30����BC��6�����ó߹滭������г�ָ�����������������г�ָ������ij��ȣ�
���𰸡���1���١����ڡ̣���2����г�ָ��ߡ��ij���Ϊ4��
��������
��1����������г�ָ������Ķ��弴���жϣ�
��2����ͼ����CAB��ƽ���ߣ�ֻҪ֤���߶�AD������г�ָ���������,������ֱ��������30������Ա���б�ߵ�һ���CD+BD=BC=6�����CD�ij��ȼ���.
��1������Ϊ���ȱ�����������һ���㣬�ָ�����������ζ���һ����С��60�㣬���������ǵȱ������Σ��ʵȱ������β����ڡ���г�ָ��ߡ�������ȷ���Ǽ����⣻
���������������һ��������һ���ǵ�������
����������αش��ڡ���г�ָ��ߡ����������£�
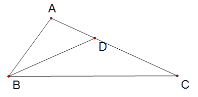
��ͼ���ڡ�ABC�У���ABC=2��C������ABC��ƽ���߽�AC��D.
��BDƽ�֡�ABC
���ABD=��DBC=![]() ,
,
�ߡ�ABC=2��C
���ABD=��DBC=��C��
��BD=DC����BDC����������
��ADB=��DBC+��C=2��C=��ABC.
��BDΪ��ABC�ĺ�г�ָ���.
��ȷ���������⣬
�ʴ�Ϊ�������̣�
��2����ͼ2������CAB��ƽ����AD��
�ߡ�C��90�㣬��B��30�㣬
���DAB����B��30�㣬
��DA��DB��
���ADB�ǵ��������Σ��ҡ�CAD����DAB����B��
���ADC����B+��BAD����CAD+��BAD����BAC
���߶�AD�ǡ�ABC�ġ���г�ָ��ߡ���
��CD��x����BD��6��x��
��![]() ��
��
��x��2��
��AD��BD��6��2��4��
����г�ָ��ߡ��ij���Ϊ4��