题目内容
下列说法中正确的个数有( )
(1)若a∥b,b∥c,则a∥c.(2)在同一平面内,不相交的两条线段必平行.(3)相等的角是对顶角.(4)两条直线被第三条直线所截,所得到同位角相等.(5)若a⊥b,b⊥c,则a⊥c.(6)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
(1)若a∥b,b∥c,则a∥c.(2)在同一平面内,不相交的两条线段必平行.(3)相等的角是对顶角.(4)两条直线被第三条直线所截,所得到同位角相等.(5)若a⊥b,b⊥c,则a⊥c.(6)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
分析:存在两种情况a、c是一条直线和a、c不是一条直线,能推出不同的结论,即可判断(1);当两两条线段在一条直线上时(举反例),两条线段不相交,也不平行,即可判断(2);根据平行线性质和对顶角性质即可判断(3);根据只有在平行线中,同位角才相等,即可判断(4);根据在同一平面内,平行线的传递性,即可求出a∥c,即可判断(5);画出图形,求出∠NEF=∠MFE,根据平行线的判定求出平行,即可判断(6).
解答:解:∵假如a和c不是一条直线时,a∥b,b∥c,能推出a∥c;而当a和c是一条直线时,a∥b,b∥c,不能推出a∥c;
∴(1)错误;
∵如图:
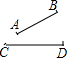
AB和CD不平行,
∴(2)错误;
∵在两条平行线被第三条直线所截的同位角相等,但不是对顶角,
∴(3)错误;
∵只有两条平行线被第三条直线所截的同位角才相等,
∴(4)错误;
∵若在同一平面内,a⊥b,b⊥c,
∴a∥c,∴(5)错误;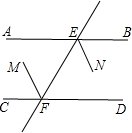
如图:∵AB∥CD,
∴∠BEF=∠CFE,
∵EN平分∠BEF,FM平分∠CFE,
∴∠NEF=
∠BEF,∠MFE=
∠CFE,
∴∠MFE=∠NEF,
∴EN∥FM,∴(6)正确.
故选A.
∴(1)错误;
∵如图:

AB和CD不平行,
∴(2)错误;
∵在两条平行线被第三条直线所截的同位角相等,但不是对顶角,
∴(3)错误;
∵只有两条平行线被第三条直线所截的同位角才相等,
∴(4)错误;
∵若在同一平面内,a⊥b,b⊥c,
∴a∥c,∴(5)错误;

如图:∵AB∥CD,
∴∠BEF=∠CFE,
∵EN平分∠BEF,FM平分∠CFE,
∴∠NEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MFE=∠NEF,
∴EN∥FM,∴(6)正确.
故选A.
点评:本题综合考查了对平行线的性质和判定的有关应用,注意两直线的位置关系有三种:平行、相交、异面;主要考查学生的理解能力和辨析能力,此题是一道比较容易出错的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目