ЬтФПФкШн
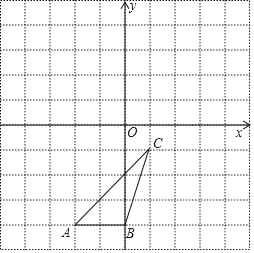
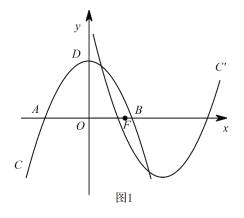
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпCЃКy=ax2+bx+cгыxжсЯрНЛгкAЃЌBСНЕуЃЌЖЅЕуЮЊD(0ЃЌ4)ЃЌAB=4![]() ЃЌЩшЕуF(mЃЌ0)ЪЧxжсЕФе§АыжсЩЯвЛЕуЃЌНЋХзЮяЯпCШЦЕуFа§зЊ180ЁуЃЌЕУЕНаТЕФХзЮяЯпC/ЃЎ
ЃЌЩшЕуF(mЃЌ0)ЪЧxжсЕФе§АыжсЩЯвЛЕуЃЌНЋХзЮяЯпCШЦЕуFа§зЊ180ЁуЃЌЕУЕНаТЕФХзЮяЯпC/ЃЎ
(1)ЧѓХзЮяЯпCЕФКЏЪ§БэДяЪНЃЛ
(2)ШєХзЮяЯпC/гыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
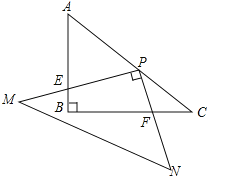
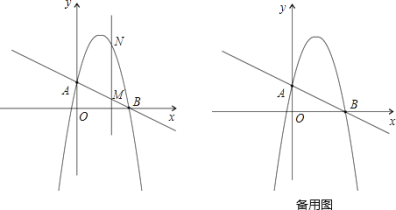
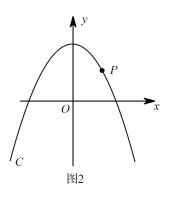
(3)ШчЭМ2ЃЌPЪЧЕквЛЯѓЯоФкХзЮяЯпCЩЯвЛЕуЃЌЫќЕНСНзјБъжсЕФОрРыЯрЕШЃЌЕуPдкХзЮяЯпC/ЩЯЕФЖдгІЕуP/ЃЌЩшMЪЧCЩЯЕФЖЏЕуЃЌNЪЧC/ЩЯЕФЖЏЕуЃЌЪдЬНОПЫФБпаЮPMP/NФмЗёГЩЮЊе§ЗНаЮЃПШєФмЃЌЧыжБНгаДГіmЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ2ЃМmЃМ
ЃЛЃЈ2ЃЉ2ЃМmЃМ![]() ЃЛЃЈ3ЃЉm=6Лђm=
ЃЛЃЈ3ЃЉm=6Лђm=![]() Љ3ЃЎ
Љ3ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉгЩЬтвтХзЮяЯпЕФЖЅЕуCЃЈ0ЃЌ4ЃЉЃЌAЃЈ![]() ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ
ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌАбAЃЈ
ЃЌАбAЃЈ![]() ЃЌ0ЃЉДњШыПЩЕУa=
ЃЌ0ЃЉДњШыПЩЕУa=![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉгЩЬтвтХзЮяЯпCЁфЕФЖЅЕузјБъЮЊЃЈ2mЃЌЉ4ЃЉЃЌЩшХзЮяЯпCЁфЕФНтЮіЪНЮЊ![]() ЃЌгЩ
ЃЌгЩ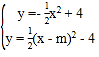 ЃЌЯћШЅyЕУЕН
ЃЌЯћШЅyЕУЕН![]() ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга
ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга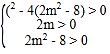 ЃЌНтВЛЕШЪНзщМДПЩНтОіЮЪЬтЃЛ
ЃЌНтВЛЕШЪНзщМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЧщаЮ1ЃЌЫФБпаЮPMPЁфNФмГЩЮЊе§ЗНаЮЃЎзїPEЁЭxжсгкEЃЌMHЁЭxжсгкHЃЎгЩЬтвтвзжЊPЃЈ2ЃЌ2ЃЉЃЌЕБЁїPFMЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЭЦГіPF=FMЃЌЁЯPFM=90ЁуЃЌвзжЄЁїPFEЁеЁїFMHЃЌПЩЕУPE=FH=2ЃЌEF=HM=2ЉmЃЌПЩЕУMЃЈm+2ЃЌmЉ2ЃЉЃЌРэгЩД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛЧщаЮ2ЃЌШчЭМЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЭЌЗЈПЩЕУMЃЈmЉ2ЃЌ2ЉmЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтХзЮяЯпЕФЖЅЕуCЃЈ0ЃЌ4ЃЉЃЌAЃЈ![]() ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ
ЃЌ0ЃЉЃЌЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌАбAЃЈ
ЃЌАбAЃЈ![]() ЃЌ0ЃЉДњШыПЩЕУa=
ЃЌ0ЃЉДњШыПЩЕУa=![]() ЃЌЁрХзЮяЯпCЕФКЏЪ§БэДяЪНЮЊ
ЃЌЁрХзЮяЯпCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЬтвтХзЮяЯпCЁфЕФЖЅЕузјБъЮЊЃЈ2mЃЌЉ4ЃЉЃЌЩшХзЮяЯпCЁфЕФНтЮіЪНЮЊ![]() ЃЌгЩ
ЃЌгЩ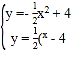 ЃЌЯћШЅyЕУЕН
ЃЌЯћШЅyЕУЕН![]() ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга
ЃЌгЩЬтвтЃЌХзЮяЯпCЁфгыХзЮяЯпCдкyжсЕФгвВргаСНИіВЛЭЌЕФЙЋЙВЕуЃЌдђга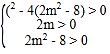 ЃЌНтЕУ2ЃМmЃМ
ЃЌНтЕУ2ЃМmЃМ![]() ЃЌЁрТњзуЬѕМўЕФmЕФШЁжЕЗЖЮЇЮЊ2ЃМmЃМ
ЃЌЁрТњзуЬѕМўЕФmЕФШЁжЕЗЖЮЇЮЊ2ЃМmЃМ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉНсТлЃКЫФБпаЮPMPЁфNФмГЩЮЊе§ЗНаЮЃЎ
РэгЩЃК1ЧщаЮ1ЃЌШчЭМЃЌзїPEЁЭxжсгкEЃЌMHЁЭxжсгкHЃЎ

гЩЬтвтвзжЊPЃЈ2ЃЌ2ЃЉЃЌЕБЁїPFMЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЁрPF=FMЃЌЁЯPFM=90ЁуЃЌвзжЄЁїPFEЁеЁїFMHЃЌПЩЕУPE=FH=2ЃЌEF=HM=2ЉmЃЌЁрMЃЈm+2ЃЌmЉ2ЃЉЃЌЁпЕуMдк![]() ЩЯЃЌЁр
ЩЯЃЌЁр![]() ЃЌНтЕУm=
ЃЌНтЕУm=![]() Љ3ЛђЉ
Љ3ЛђЉ![]() Љ3ЃЈЩсЦњЃЉЃЌЁрm=
Љ3ЃЈЩсЦњЃЉЃЌЁрm=![]() Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
ЧщаЮ2ЃЌШчЭМЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЌЭЌЗЈПЩЕУMЃЈmЉ2ЃЌ2ЉmЃЉЃЌАбMЃЈmЉ2ЃЌ2ЉmЃЉДњШы![]() жаЃЌ
жаЃЌ![]() ЃЌНтЕУm=6Лђ0ЃЈЩсЦњЃЉЃЌЁрm=6ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
ЃЌНтЕУm=6Лђ0ЃЈЩсЦњЃЉЃЌЁрm=6ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
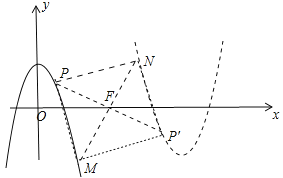
злЩЯЫљЪіЃКm=6Лђm=![]() Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ
Љ3ЪБЃЌЫФБпаЮPMPЁфNЪЧе§ЗНаЮЃЎ

 ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈУћаЃЯЕСаД№АИЁОЬтФПЁПМзЁЂввСНУћЭЌбЇНјааЩфЛїбЕСЗЃЌдкЯрЭЌЬѕМўЯТИїЩфАа5ДЮЃЌГЩМЈЭГМЦШчЯТБэЃК
УќжаЛЗЪ§ | 7 | 8 | 9 | 10 |
МзУќжаЯргІЛЗЪ§ЕФДЮЪ§ | 2 | 2 | 0 | 1 |
ввУќжаЯргІЛЗЪ§ЕФДЮЪ§ | 1 | 3 | 1 | 0 |
(1)ЧѓМзЁЂввСНШЫЩфЛїГЩМЈЕФЦНОљЪ§ЃЛ
(2)МзЁЂввСНШЫжаЃЌЫЕФЩфЛїГЩМЈИќЮШЖЈаЉ?ЧыЫЕУїРэгЩЃЎ