题目内容
【题目】已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( ).
A.( ![]() ,-4)
,-4)
B.( ![]() ,0)
,0)
C.( ![]() ,0)
,0)
D.( ![]() ,0)
,0)
【答案】C
【解析】解答:∵PM+PN最短,
∴M、P、N三点共线,
∵M(3,5),N(1,-1),
∴设解析式为y=kx+b,
把M(3,5),N(1,-1)分别代入解析式得,![]() ,
,
解得 ![]() ,
,
其解析式为y=3x-4.
当y=0时,x= ![]() .
.
故P点坐标为( ![]() ,0).
,0).
故选C.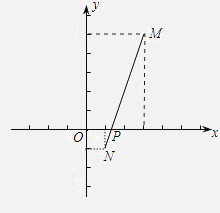
分析:若PM+PN最短,则M、P、N三点共线,根据M、N的坐标,求出MN的解析式,再求出与x轴的交点即可.
【考点精析】本题主要考查了确定一次函数的表达式和轴对称-最短路线问题的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.

练习册系列答案
相关题目