题目内容
如图,线段AC和BD相交于O,且都被点O平分,你能得到AB∥CD吗?
请说明理由.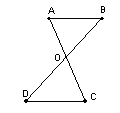
请说明理由.

见解析
证明:∵AC和BD相交于O,且被点O平分,
∴OA=OC,OB=OD,
在△AOC和△BOD中,
OA=OC ∠AOB=∠COD 0B=OD ,
∴△AOC≌△BOD,
∴AB=CD,∠A=∠C,
∴AB∥CD.
根据两边及其夹角相等的两个三角形全等,可证得△AOB≌△COD,可得AB=CD,∠A=∠C,根据内错角相等,两直线平行,即可证得AB∥CD
∴OA=OC,OB=OD,
在△AOC和△BOD中,
OA=OC ∠AOB=∠COD 0B=OD ,
∴△AOC≌△BOD,
∴AB=CD,∠A=∠C,
∴AB∥CD.
根据两边及其夹角相等的两个三角形全等,可证得△AOB≌△COD,可得AB=CD,∠A=∠C,根据内错角相等,两直线平行,即可证得AB∥CD

练习册系列答案
相关题目

 与
与 是
是
 B=
B=