题目内容
学校要在长为30米，宽为20米的矩形空地上修筑两条同样宽且互相垂直的道路，剩余的部分种草，使得种草的面积为504平方米，问道路的宽应为多少米．
解：设道路的宽是x米，
（30-x）（20-x）=504，
600-30x-20x+x2=504，
x2-50x+96=0，
（x-48）（x-2）=0
x-48=0，x-2=0
x1=48（舍）x2=2，
答：道路的宽是2米．
分析：把四块耕地拼到一起正好构成一个矩形，矩形的长和宽分别是（30-x）和（20-x），根据矩形的面积公式，列出关于道路宽的方程求解．
点评：本题考查了一元二次方程的应用，关键将四个矩形恰当的方式拼成大矩形列出等量关系．
（30-x）（20-x）=504，
600-30x-20x+x2=504，
x2-50x+96=0，
（x-48）（x-2）=0
x-48=0，x-2=0
x1=48（舍）x2=2，
答：道路的宽是2米．
分析：把四块耕地拼到一起正好构成一个矩形，矩形的长和宽分别是（30-x）和（20-x），根据矩形的面积公式，列出关于道路宽的方程求解．
点评：本题考查了一元二次方程的应用，关键将四个矩形恰当的方式拼成大矩形列出等量关系．
练习册系列答案
相关题目
学校要在长为30米，宽为20米的矩形空地上修筑两条同样宽且互相垂直的道路，剩余的部分种草，使得种草的面积为504平方米，问道路的宽应为多少米．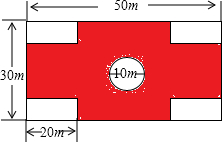
剑川县某学校要在教学楼前铺设小广场地面，其图案设计如下图所示．若长方形地面的长为50米，宽为30米，中心建一个直径为10米的圆形喷泉，四周各角留一个长20米，宽5米的小长方形花坛，图中阴影处铺设广场地砖．
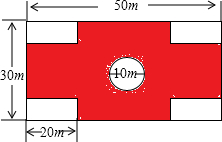剑川县某学校要在教学楼前铺设小广场地面，其图案设计如下图所示．若长方形地面的长为50米，宽为30米，中心建一个直径为10米的圆形喷泉，四周各角留一个长20米，宽5米的小长方形花坛，图中阴影处铺设广场地砖．