题目内容
剑川县某学校要在教学楼前铺设小广场地面，其图案设计如下图所示．若长方形地面的长为50米，宽为30米，中心建一个直径为10米的圆形喷泉，四周各角留一个长20米，宽5米的小长方形花坛，图中阴影处铺设广场地砖．（1）求阴影部分的面积S（π取3）；
（2）甲、乙两人承包了铺设地砖的任务，若甲单独做需20小时完成，乙单独做需要12小时完成；甲乙二人合做6小时后，乙有事离开，剩下的由甲单独完成．请你根据所给的条件提出一个问题，并列方程解答．
问题：
甲还需多长时间才能完成？
甲还需多长时间才能完成？
．分析：（1）先计算出长方形的面积，然后减去4个小长方形和圆的面积；
（2）可以提出，甲还需多长时间才能完成，根据题中条件，可以设甲还需x小时才能完成，等量关系为：甲乙合作完成的+甲单独完成的=整个任务量，根据此列出方程式并解答．
（2）可以提出，甲还需多长时间才能完成，根据题中条件，可以设甲还需x小时才能完成，等量关系为：甲乙合作完成的+甲单独完成的=整个任务量，根据此列出方程式并解答．
解答：解：（1）大长方形的面积为：50×30=1500（平方米），
小长方形的面积为：20×5=100（平方米），
圆的面积为：5×5×3=75（平方米），
所以阴影部分面积为：S=1500-100×4-75=1025（平方米），
答：阴影部分面积是1025平方米；
（2）设甲单独完成还需x小时，
根据题意可列出方程式：x÷20+6÷20+6÷12=1，
解得：x=4，
答：甲还需要4个小时才能完成．
小长方形的面积为：20×5=100（平方米），
圆的面积为：5×5×3=75（平方米），
所以阴影部分面积为：S=1500-100×4-75=1025（平方米），
答：阴影部分面积是1025平方米；
（2）设甲单独完成还需x小时，
根据题意可列出方程式：x÷20+6÷20+6÷12=1，
解得：x=4，
答：甲还需要4个小时才能完成．
点评：此题主要考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
练习册系列答案
相关题目
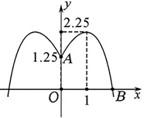19、某学校要在圆形水池的中心点O处安装水管OA=1.25米，要建音乐喷泉，其水流路径呈抛物线型（如图），且在离O点1米处水喷得最高2.25米，要使水流不溅到池外，水池的半径应不少于多少米？
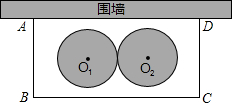某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙（墙的长度不限），另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD．已知木栏总长为120米，设AB边的长为x米，长方形ABCD的面积为S平方米．
和
，且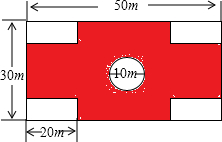
剑川县某学校要在教学楼前铺设小广场地面，其图案设计如下图所示．若长方形地面的长为50米，宽为30米，中心建一个直径为10米的圆形喷泉，四周各角留一个长20米，宽5米的小长方形花坛，图中阴影处铺设广场地砖．