题目内容
【题目】已知等边三角形ABC的边长为8,P是BC边上一点,连接AP,若AP=7,则BP的长为 .
【答案】3或5
【解析】解:如图1所示, 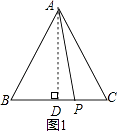
过点A作AD⊥BC,
设DP=x,
∵△ABC为等边三角形,AD⊥BC,
∴BD= ![]() =4,
=4,
在Rt△ABD中,
AD2=AB2﹣BD2=82﹣42=48,
在Rt△APD中,
DP2=AP2﹣AD2=72﹣48=1,
∴DP=1,
∴BP=5;
当点P在AD的左侧时,如图2所示,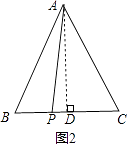
同理可得,BP=BD﹣PD=4﹣1=3,
综上所述,BP的长为3或5,
所以答案是:3或5.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目