��Ŀ����
����Ŀ����֪����ͼ1������AB��CD����CAB�Ľ�ƽ���߽�����CD�ڵ�P1 �� 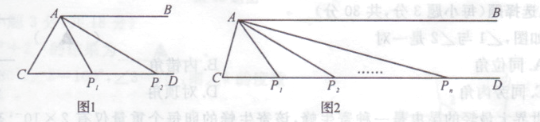
��1������C=50�㣬���AP1C�Ķ�����
��2����ͼ1������P1AB�Ľ�ƽ���߽�����CD�ڵ�P2 �� �����AP1C���AP2C��������ϵ����˵�����ɣ�
��3����ͼ2����(2)�������£�����������P2AB�Ľ�ƽ����AP3 �� ��P3AB�Ľ�ƽ����AP4 �� ��������Pn-1AB�Ľ�ƽ����APn �� ���е�P3,P4����Pn-1Pn��������CD�ϣ�����APnC=x��ֱ��д����C�Ķ���(�ú�x�Ĵ���ʽ��ʾ)��
���𰸡�
��1��
�⣺��AB//CD��
���C+��BAC=180�㣬
���BAC=180��-50��=130�㣬
��AP1ƽ�֡�BAC��
���BAP1= ![]() ��BAC=65�㣬
��BAC=65�㣬
��AB//CD��
���AP1C=��BAP1=65��.
��2��
�⣺���룺��AP1C=2��AP2C.
���ɣ���ΪP2Aƽ�֡�P1AB��
���ԡ�P2AB= ![]() ��P1AB=
��P1AB= ![]() ��AP1C��
��AP1C��
��ΪAB//CD��
���ԡ�AP2C=��P2AB= ![]() ��AP1C��
��AP1C��
����AP1C=2��AP2C.
��3��
�⣺�ɣ�1���ͣ�2���ɵ�
��AP1C=��P1AB= ![]() ��CAB=
��CAB= ![]() ��180��-��C����
��180��-��C����
��AP2C= ![]() ��AP1C=
��AP1C= ![]() ��
��
����
��APnC= ![]() =x����á�C=180��-2n��x.
=x����á�C=180��-2n��x.
������������ƽ���ߵ����ʡ���ֱ��ƽ�У�ͬ���ڽǻ������ڽǴ���ȡ������ƽ���ߵĶ��岻�ܵõ����ɡ�APnC= ![]() ��AP1C=
��AP1C= ![]() .
.
�����㾫��������ƽ���ߵ������ǽ����ĸ�������Ҫ֪����ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����

 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�����Ŀ��Ϊ����ͬѧ���˽��Լ�������ˮƽ������1�����������ʦ��ȫ��45��ѧ��������һ������ģ����ԣ��÷־�Ϊ�������ɼ�����Ϊ10�֣��ɼ��ﵽ9�����ϣ�����9�֣�Ϊ���㣬�ɼ��ﵽ6�����ϣ�����6�֣�Ϊ�ϸ�1�������ίԱ������β��Գɼ���������ͳ��ͼ�ͷ��������£� 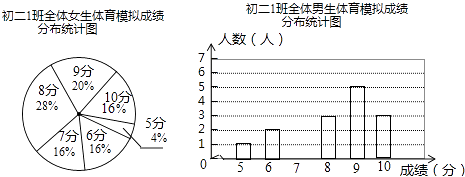
����1������ģ����Գɼ�������
ƽ���� | ���� | ��λ�� | ���� | �ϸ��� | ������ | |
���� | 2 | 8 | 7 | 95% | 40% | |
�� | 7.92 | 1.99 | 8 | 96% | 36% |
����������Ϣ������������⣺
��1������β����У��ð�Ů����10�ֵ�����Ϊ4�ˣ���������Ů���ˣ�
��2����ȫ����1����������ģ����Գɼ�ͳ��ͼ��������Ӧ�����ݱ�ע��ͳ��ͼ�ϣ�
��3����ȫ����1������ģ����Գɼ���������
��4������Ϊ��������������У�1��������ӡ�Ů�����ĸ����ָ�ͻ��һЩ����д��һ��֧����Ŀ��������ɣ�
��5����������ʦ˵�������忴��1��������ɼ��ںϸ��ʷ��������꣬���������ʷ��滹�������룬�����ϣ��ȫ��ͬѧ������ǿ������������ȡ����ĩ�����У�ȫ��������ʴﵽ60%����������������������6�ˣ���Ů���������������Ӷ����˲�����ɿ���ʦ�����Ŀ�ꣿ
