题目内容
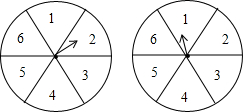
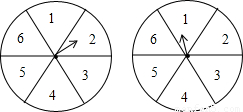
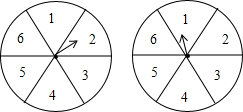
现有一项资助灾区的公益活动,每位参与者需交赞助费50元,参与者转动两个转盘,转盘停止后,指针各指向一个数字区域.若数字和为12则获得一等奖,奖金200元,和为9则获得二等奖,奖金100元,数字和为7则获得三等奖,奖金50元,其余不得奖.此次活动所集赞助费除支付获奖奖金外,余下的全部用于资助灾区.(1)求每位参与者获得一等奖、二等奖、三等奖的概率分别是多少?(用列举法求解)
(2)若此次活动有2000人参加,活动结束有多少赞助费用于资助灾区?
分析:(1)列举出所有情况,看获得一等奖、二等奖、三等奖的情况数占总情况数的多少即可;
(2)获奖钱数=总赞助费×相应概率;让总赞助费减去总获奖的钱数即为活动结束有多少赞助费用于资助灾区.
(2)获奖钱数=总赞助费×相应概率;让总赞助费减去总获奖的钱数即为活动结束有多少赞助费用于资助灾区.
解答:解:(1)列表如下: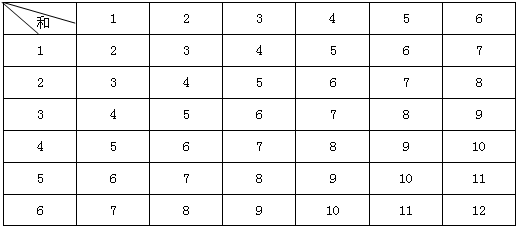
∴P(获得一等奖)=
,
P(获得二等奖)=
=
,
P(获得三等奖)=
=
;
(2)(
×200+
×100+
×50)×2000=50000,
2000×50-50000=50000(元)
∴活动结束有50000元赞助费用于资助灾区.

∴P(获得一等奖)=
| 1 |
| 36 |
P(获得二等奖)=
| 4 |
| 36 |
| 1 |
| 9 |
P(获得三等奖)=
| 6 |
| 36 |
| 1 |
| 6 |
(2)(
| 1 |
| 36 |
| 1 |
| 9 |
| 1 |
| 6 |
2000×50-50000=50000(元)
∴活动结束有50000元赞助费用于资助灾区.
点评:考查有关概率的一些计算;用到的知识点为:概率等于所求情况数与总情况数之比.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目