题目内容
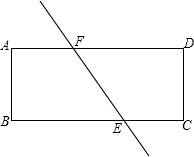
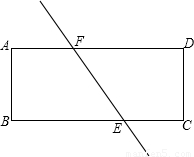
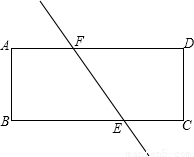
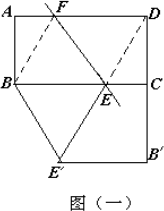
如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合),设AD=a,AB=b,BE=x.
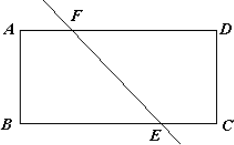
(Ⅰ)求证:AF=EC;
(Ⅱ)用剪刀将纸片沿直线EF剪开后,再将纸片ABEF沿AB对称翻折,然后平移拼接在梯形ECDF的下方,使一底边重合,直腰落在边DC的延长线上,拼接后,下方的梯形记作E![]() ′C,连结B
′C,连结B![]() .
.
(1)当直线EE′经过原矩形的顶点A时,求出所对应的x∶a的值;
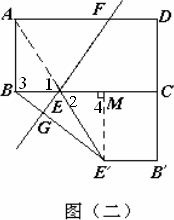
(2)当直线EE′经过原矩形的顶点D时,请你说明当a与b满足什么关系时,B![]() ⊥EF.
⊥EF.
答案:
解析:
解析:
|
(Ⅰ)证明:∵AD=a,AB=b,BE=x,S梯形ABEF=S梯形CDFE. ∴ ∴2AF=EC+(a-x). 又∵EC=a-x, ∴2AF=2E (Ⅱ)解:(1)当直线E
∵EC∥ ∴ 由EC=a-x, D 得 ∴x∶a= ∴B (2)如图(二),当直线E
过点 在 ∴EM= 若B 又∵∠BEG=∠FEC=∠2,∠2+∠M 在Rt△BME′中,tan∠ 在Rt△EME′中,tan∠M ∴ 注:与本答案不同的正确解法,请参照给分. |

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
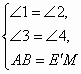
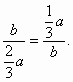 又∵a>0,b>0,
又∵a>0,b>0,