题目内容
在直角坐标系中，O为坐标原点，A（-2，2），在x轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有
- A.1个
- B.2个
- C.3个
- D.4个
D
分析：使△AOP为等腰三角形，只需分两种情况考虑：OA当底边或OA当腰．当OA是底边时，则点P即为OA的垂直平分线和x轴的交点；当OA是腰时，则点P即为分别以O、A为圆心，以OA为半径的圆和x轴的交点（点O除外）．
解答：（1）若AO作为腰时，有两种情况，当A是顶角顶点时，P是以A为圆心，以OA为半径的圆与x轴的交点，共有1个，若OA是底边时，P是OA的中垂线与x轴的交点，有1个
当O是顶角顶点时，P是以O为圆心，以OA为半径的圆与x轴的交点，有1个；
（2）若OA是底边时，P是OA的中垂线与x轴的交点，有1个．
以上4个交点没有重合的．故符合条件的点有4个．
故选D．
点评：此题主要考查了坐标与图形的性质及等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．
分析：使△AOP为等腰三角形，只需分两种情况考虑：OA当底边或OA当腰．当OA是底边时，则点P即为OA的垂直平分线和x轴的交点；当OA是腰时，则点P即为分别以O、A为圆心，以OA为半径的圆和x轴的交点（点O除外）．
解答：（1）若AO作为腰时，有两种情况，当A是顶角顶点时，P是以A为圆心，以OA为半径的圆与x轴的交点，共有1个，若OA是底边时，P是OA的中垂线与x轴的交点，有1个
当O是顶角顶点时，P是以O为圆心，以OA为半径的圆与x轴的交点，有1个；
（2）若OA是底边时，P是OA的中垂线与x轴的交点，有1个．
以上4个交点没有重合的．故符合条件的点有4个．
故选D．
点评：此题主要考查了坐标与图形的性质及等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
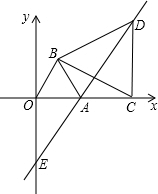OAB，C为x轴正半轴上的一个动点（OC＞1），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．
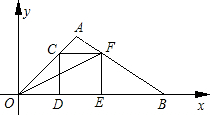在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF．连接AF并延长交x轴的正半轴于点B，连接OF，设OD=t．
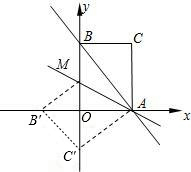点B′处，C的对应点为C′．