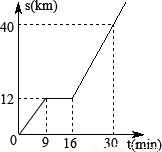
题目内容
(2004•河北)如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)

【答案】分析:(1)根据平移的性质与轴对称图形的性质,可得答案;
(2)根据题意,先设平移平移时间为x秒,进而可得关系式y=2x+40;(0≤x≤16);即可得出y取得最大值和最小值时x的值;
(3)与(2)的方法类似,注意面积计算方法的不同即可.
解答:解:(1)如图1,△A2B2C2是△A1B1C1关于直线QN成轴对称的图形
 ;
;
(2)当△ABC以每秒1个单位长的速度向下平移x秒时(如图2),
则有:MA=x,MB=x+4,MQ=20,
y=S梯形QMBC-S△AMQ-S△ABC
= (4+20)(x+4)-
(4+20)(x+4)- ×20x-
×20x- ×4×4
×4×4
=2x+40(0≤x≤16).(6分)
由一次函数的性质可知:
当x=0时,y取得最小值,且y最小=40,
当x=16时,y取得最大值,且y最大=2×16+40=72;(8分)
(3)解法一:
当△ABC继续以每秒1个单位长的速度向右平移时,
此时16≤x≤32,PB=20-(x-16)=36-x,PC=PB-4=32-x,
∴y=S梯形BAQP-S△CPQ-S△ABC= (4+20)(36-x)-
(4+20)(36-x)- ×20×(32-x)-
×20×(32-x)- ×4×4
×4×4
=-2x+104(16≤x≤32).(10分)
由一次函数的性质可知:
当x=32时,y取得最小值,且y最小=-2×32+104=40;
当x=16时,y取得最大值,且y最大=-2×16+104=72.(12分)
解法二:
在△ABC自左向右平移的过程中,
△QAC在每一时刻的位置都对应着(2)中△QAC某一时刻的位置,
使得这样的两个三角形关于直线QN成轴对称.
因此,根据轴对称的性质,
只需考查△ABC在自上至下平移过程中△QAC面积的变化情况,
便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况.(10分)(另加2分)
当x=16时,y取得最大值,且y最大=72,
当x=32时,y取得最小值,且y最小=40.(12分)(再加2分)
说明:(1)本题解法较多,对于其他正确解法,请参照评分标准按步骤给分;
(2)对于(3),如果学生按照解法一的方法求解,不加分.如果按照解法二利用图形变换的方法说明,可考虑加1~4分.
点评:本题考查平移的基本性质与运用:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
(2)根据题意,先设平移平移时间为x秒,进而可得关系式y=2x+40;(0≤x≤16);即可得出y取得最大值和最小值时x的值;
(3)与(2)的方法类似,注意面积计算方法的不同即可.
解答:解:(1)如图1,△A2B2C2是△A1B1C1关于直线QN成轴对称的图形
 ;
;(2)当△ABC以每秒1个单位长的速度向下平移x秒时(如图2),
则有:MA=x,MB=x+4,MQ=20,
y=S梯形QMBC-S△AMQ-S△ABC
=
 (4+20)(x+4)-
(4+20)(x+4)- ×20x-
×20x- ×4×4
×4×4=2x+40(0≤x≤16).(6分)
由一次函数的性质可知:
当x=0时,y取得最小值,且y最小=40,
当x=16时,y取得最大值,且y最大=2×16+40=72;(8分)
(3)解法一:
当△ABC继续以每秒1个单位长的速度向右平移时,
此时16≤x≤32,PB=20-(x-16)=36-x,PC=PB-4=32-x,
∴y=S梯形BAQP-S△CPQ-S△ABC=
 (4+20)(36-x)-
(4+20)(36-x)- ×20×(32-x)-
×20×(32-x)- ×4×4
×4×4=-2x+104(16≤x≤32).(10分)
由一次函数的性质可知:
当x=32时,y取得最小值,且y最小=-2×32+104=40;
当x=16时,y取得最大值,且y最大=-2×16+104=72.(12分)
解法二:
在△ABC自左向右平移的过程中,
△QAC在每一时刻的位置都对应着(2)中△QAC某一时刻的位置,
使得这样的两个三角形关于直线QN成轴对称.
因此,根据轴对称的性质,
只需考查△ABC在自上至下平移过程中△QAC面积的变化情况,
便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况.(10分)(另加2分)
当x=16时,y取得最大值,且y最大=72,
当x=32时,y取得最小值,且y最小=40.(12分)(再加2分)
说明:(1)本题解法较多,对于其他正确解法,请参照评分标准按步骤给分;
(2)对于(3),如果学生按照解法一的方法求解,不加分.如果按照解法二利用图形变换的方法说明,可考虑加1~4分.
点评:本题考查平移的基本性质与运用:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
相关题目
(2004•河北)如图1是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据:
(1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;
(2)①填写下表:
②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数的表达式:______;
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?

| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
(2)①填写下表:
| x | 5 | 10 | 20 | 30 | 40 | 50 |
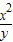 |
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?

(2004•河北)如图1是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据:
(1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;
(2)①填写下表:
②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数的表达式:______;
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?

| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
(2)①填写下表:
| x | 5 | 10 | 20 | 30 | 40 | 50 |
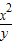 |
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?

(2004•河北)如图1是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据:
(1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;
(2)①填写下表:
②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数的表达式:______;
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?

| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
(2)①填写下表:
| x | 5 | 10 | 20 | 30 | 40 | 50 |
 |
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?

(2004•河北)如图1是某段河床横断面的示意图.查阅该河段的水文资料,得到下表中的数据:
(1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;
(2)①填写下表:
②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数的表达式:______;
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?

| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
(2)①填写下表:
| x | 5 | 10 | 20 | 30 | 40 | 50 |
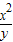 |
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?