题目内容
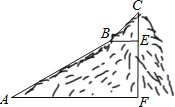
【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)求证:四边形DEBF是菱形;
(2)若AB=8,AD=4,求四边形BEDF的面积.
【答案】(1)详见解析;(2)80
【解析】
(1)首先根据矩形性质得出AD∥BC,从而得出∠EDB=∠DBC,然后结合折叠性质可知∠DBG=∠DBC,据此进一步证明出DE=BE,最后通过证明四边形BEDF为平行四边形进一步证明其是菱形即可;
(2)设菱形BEDF的边长为![]() ,则AE=DEAD=
,则AE=DEAD=![]() ,根据勾股定理求出
,根据勾股定理求出![]() 的值,然后进一步加以计算即可.
的值,然后进一步加以计算即可.
(1)证明:
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC,
根据折叠性质可知:∠DBG=∠DBC,
∴∠EDB=∠EBD,
∴DE=BE,
∵AD∥BC,DF∥BE,
∴四边形BEDF为平行四边形,
又∵DE=BE,
∴四边形BEDF为菱形;
(2)设菱形BEDF的边长为![]() ,则AE=DEAD=
,则AE=DEAD=![]() ,
,
在Rt△AEB中,![]() ,
,
即:![]()
解得:![]() ,
,
∴菱形BEDF的面积=DE×AB=10×8=80.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目