题目内容
已知AB、CD分别是梯形ABCD的上、下底，且AB=8，EF是梯形的中位线长为12，则CD=
16
16
．分析：根据梯形的中位线长等于两底和的一半，进行计算．
解答：解：∵由梯形的中位线定理得：EF=
（AB+CD），
∴CD=2EF-AB=2×12-8=16，
故答案为：16．
| 1 |
| 2 |
∴CD=2EF-AB=2×12-8=16，
故答案为：16．
点评：本题考查的是梯形中位线的性质，属最基本的概念题目．
练习册系列答案
相关题目
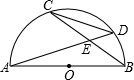如图，已知AB，CD分别是半圆O的直径和弦，AD和BC相交于点E，若∠AEC=α，则S△CDE：S△ABE等于（ ）| A、sinα | B、cosα | C、sin2α | D、cos2α |