Question

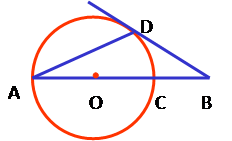
如图，线段AB经过圆心O，交⊙O于点A、C，∠BAD=∠B=30°，边BD交圆于点D．
（1）求证：BD是⊙O的切线．
（2）若⊙O的半径为2，求弦AD的长．

Answer 1

分析：（1）因为D在圆上，所以证∠BDO=90°即可．
（2）作OE⊥AD与AD，构造直角三角形AEO，再利用解直角三角形的知识解答．

解答：（1）证明：∵∠BAD=30°，OA=OD，
∴∠ADO=∠BAD=30°，
∴∠BOD=60°．
在Rt△BOD中，∠B=30°，∠BOD=60°，
∴∠BDO=90°．
∴BD是⊙O的切线；

（2）作OE⊥AD，
∵∠DAB=30°，AO=2，
∴AE=2cos30°=2×

3

2

=

3

，
∴根据垂径定理，AD=2×

3

=2

3

．

点评：本题考查了切线的判定定理和垂径定理，①掌握切线的判定定理：经过半径外端且垂直于该半径的直线是圆的切线．②掌握垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．