题目内容
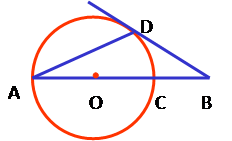
 如图,线段AB经过圆心O,交⊙O于点A、C,BD是⊙O的切线.∠BAD=30°,边BD交圆于点D,求∠B.
如图,线段AB经过圆心O,交⊙O于点A、C,BD是⊙O的切线.∠BAD=30°,边BD交圆于点D,求∠B.分析:由OA=OD∠ADO=∠BAD=30°,根据三角形外角性质得∠BOD=60°,再根据切线的性质得到OD⊥BD,则∠BDO=90°,然后利用互余计算∠B的度数.
解答:解:∵OA=OD,
∴∠ADO=∠BAD=30°,
∴∠BOD=60°
∵BD是⊙O的切线,
∴OD⊥BD,
∴∠BDO=90°,
∴∠B=90°-∠BOD=90°-60°=30°.
∴∠ADO=∠BAD=30°,
∴∠BOD=60°
∵BD是⊙O的切线,
∴OD⊥BD,
∴∠BDO=90°,
∴∠B=90°-∠BOD=90°-60°=30°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 22、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D,求证BD是⊙O的切线.
22、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D,求证BD是⊙O的切线. 如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30°,圆的半径R.
如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30°,圆的半径R. 如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D.
如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D.