ЬтФПФкШн
ЁОЬтФПЁПЃЈФЃаЭНЈСЂЃЉ
(1)ШчЭМ1ЃЌЕШбќRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌCBЃНCAЃЌжБЯпEDОЙ§ЕуCЃЌЙ§ЕуAзїADЁЭEDгкЕуDЃЌЙ§ЕуBзїBEЁЭEDгкЕуEЃЌЧѓжЄЃКЁїBECЁеЁїCDAЃЛ

ЃЈФЃаЭгІгУЃЉ
ЃЈ2)ШчЭМ2ЃЌвбжЊжБЯп11ЃКyЃН2xЃЋ3гыxжсНЛгкЕуAЁЂгыyжсНЛгкЕуBЃЌНЋжБЯп11ШЦЕуAФцЪБеыа§зЊ45ЁужСжБЯп12ЃЛЧѓжБЯп12ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЦНУцжБНЧзјБъЯЕФкгавЛЕуBЃЈ3ЃЌЃ4ЃЉЃЌЙ§ЕуBзїBAЁЭxжсгкЕуAЁЂBCЁЭyжсгкЕуCЃЌЕуPЪЧЯпЖЮABЩЯЕФЖЏЕуЃЌЕуDЪЧжБЯпyЃНЃ2xЃЋ1ЩЯЕФЖЏЕуЧвдкЕкЫФЯѓЯоФкЃЎЪдЬНОПЁїCPDФмЗёГЩЮЊЕШбќжБНЧШ§НЧаЮ?ШєФмЃЌЧѓГіЕуDЕФзјБъЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ;ЃЈ3ЃЉФмЃЌЕуDЕФзјБъЮЊ
;ЃЈ3ЃЉФмЃЌЕуDЕФзјБъЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩДЙжБЕФЖЈвхЕУЁЯADC=ЁЯCEB=90ЁуЃЌЦННЧЕФЖЈвхКЭЭЌНЧЕФгрНЧЕФЯрЕШЧѓГіЁЯDAC=ЁЯECBЃЌНЧНЧБпжЄУїЁїCDAЁеЁїBECЃЛ
ЃЈ2ЃЉжЄУїЁїABOЁеЁЯBCDЃЌЧѓГіЕуCЕФзјБъЮЊЃЈ-3ЃЌ5ЃЉЃЌгЩЕуЕНжБЯпЩЯЙЙНЈЖўдЊвЛДЮЗНГЬзщЧѓГіk=-5ЃЌb=-10ЃЌД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпl2ЕФКЏЪ§БэДяЪНЮЊy=-5x-10ЃЛ
ЃЈ3ЃЉЙЙНЈЁїMCPЁеЁїHPDЃЌгЩЦфаджЪЃЌЕуDдкжБЯпy=-2x+1ЧѓГіm=![]() Лђn=0Лђ-
Лђn=0Лђ-![]() ЃЌНЋmЕФжЕДњШыЕуDзјБъЕУЃЈ
ЃЌНЋmЕФжЕДњШыЕуDзјБъЕУЃЈ![]() ЃЌ-
ЃЌ-![]() ЃЉЛђЃЈ4ЃЌ-7ЃЉЛђЃЈ
ЃЉЛђЃЈ4ЃЌ-7ЃЉЛђЃЈ![]() ЃЌ-
ЃЌ-![]() ЃЉЃЎ
ЃЉЃЎ
НтЃКЃЈ1ЃЉШчЭМЃК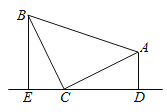
ЁпADЁЭEDЃЌBEЁЭEDЃЌ
ЁрЁЯADC=ЁЯCEB=90ЁуЃЌ
гжЁпЁЯACD+ЁЯACB+ЁЯBEC=180ЁуЃЌЁЯACB=90ЁуЃЌ
ЁрЁЯACD+ЁЯBEC=90ЁуЃЌ
гжЁпЁЯACD+ЁЯDAC=90ЁуЃЌ
ЁрЁЯDAC=ЁЯECBЃЌ
дкЁїCDAКЭЁїBECжаЃЌ
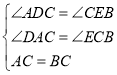
ЁрЁїCDAЁеЁїBECЃЈAASЃЉЃЛ
ЃЈ2ЃЉЙ§ЕуBзїBCЁЭABНЛACгкЕуCЃЌCDЁЭyжсНЛyжс
гкЕуDЃЌШчЭМ2ЫљЪОЃК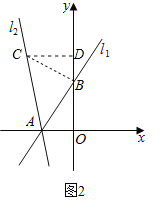
ЁпCDЁЭyжсЃЌxжсЁЭyжсЃЌ
ЁрЁЯCDB=ЁЯBOA=90ЁуЃЌ
гжЁпBCЁЭABЃЌ
ЁрЁЯABC=90ЁуЃЌ
гжЁпЁЯABO+ЁЯABC+ЁЯCBD=180ЁуЃЌ
ЁрЁЯABO+ЁЯCBD=90ЁуЃЌ
гжЁпЁЯBAO+ЁЯABO=90ЁуЃЌ
ЁрЁЯBAO=ЁЯCBDЃЌ
гжЁпЁЯBAC=45ЁуЃЌ
ЁрЁЯACB=45ЁуЃЌ
ЁрAB=CBЃЌ
дкЁїABOКЭЁЯBCDжаЃЌ
ЁрAO=BDЃЌBO=CDЃЌ
гжЁпжБЯпl1ЃКy=2x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌ
ЁрЕуAЁЂBСНЕуЕФзјБъЗжБ№ЮЊЃЈ![]() ЃЌ0ЃЉЃЌЃЈ0ЃЌ3ЃЉЃЌ
ЃЌ0ЃЉЃЌЃЈ0ЃЌ3ЃЉЃЌ
ЁрAO=![]() ЃЌBO=3ЃЌ
ЃЌBO=3ЃЌ
ЁрBD=![]() ЃЌCD=3ЃЌ
ЃЌCD=3ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ-3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Щшl2ЕФКЏЪ§БэДяЪНЮЊy=kx+bЃЈkЁй0ЃЉЃЌ
ЕуAЁЂCСНЕудкжБЯпl2ЩЯЃЌвРЬтвтЕУЃК
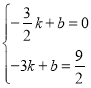 ЃЌНтЕУЃК
ЃЌНтЕУЃК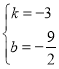
l2ЕФКЏЪ§БэДяЪНЮЊ:![]()
ЃЈ3ЃЉФмГЩЮЊЕШбќжБНЧШ§НЧаЮЃЌвРЬтвтЕУЃЌ
ЂйШєЕуPЮЊжБНЧЪБЃЌШчЭМ3МзЫљЪОЃК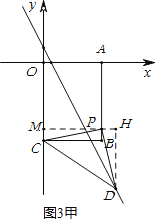
ЩшЕуPЕФзјБъЮЊЃЈ3ЃЌmЃЉЃЌдђPBЕФГЄЮЊ4+mЃЌ
ЁпЁЯCPD=90ЁуЃЌCP=PDЃЌ
ЁЯCPM+ЁЯCDP+ЁЯPDH=180ЁуЃЌ
ЁрЁЯCPM+ЁЯPDH=90ЁуЃЌ
гжЁпЁЯCPM+ЁЯDPM=90ЁуЃЌ
ЁрЁЯPCM=ЁЯPDHЃЌ
дкЁїMCPКЭЁїHPDжаЃЌ
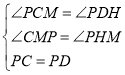
ЁрЁїMCPЁеЁїHPDЃЈAASЃЉЃЌ
ЁрCM=PHЃЌPM=PDЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ7+mЃЌ-3+mЃЉЃЌ
гжЁпЕуDдкжБЯпy=-2x+1ЩЯЃЌ
Ёр-2ЃЈ7+mЃЉ+1=-3+mЃЌ
НтЕУЃК![]()
МДЕуDЕФзјБъЮЊ![]()
ЂкШєЕуCЮЊжБНЧЪБЃЌШчЭМЫљЪОЃК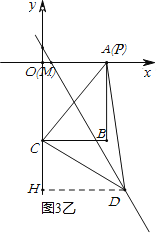
ЩшЕуPЕФзјБъЮЊЃЈ3ЃЌnЃЉЃЌдђPBЕФГЄЮЊ4+nЃЌ
CA=CDЃЌ
ЭЌРэПЩжЄУїЁїPCMЁеЁїCDHЃЈAASЃЉЃЌ
ЁрPM=CHЃЌMC=HDЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ4+nЃЌ-7ЃЉЃЌ
гжЁпЕуDдкжБЯпy=-2x+1ЩЯЃЌ
Ёр-2ЃЈ4+nЃЉ+1=-7ЃЌ
НтЕУЃКn=0ЃЌ
ЁрЕуPгыЕуAжиКЯЃЌЕуMгыЕуOжиКЯЃЌ
МДЕуDЕФзјБъЮЊЃЈ4ЃЌ-7ЃЉЃЛ
ЂлШєЕуDЮЊжБНЧЪБЃЌШчЭМЫљЪОЃК
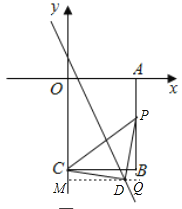
ЩшЕуPЕФзјБъЮЊЃЈ3ЃЌkЃЉЃЌдђPBЕФГЄЮЊ4+kЃЌ
CD=PDЃЌ
ЭЌРэПЩжЄУїЁїCDMЁеЁїPDQЃЈAASЃЉЃЌ
ЁрMD=PQЃЌMC=DQЃЌ
ЁрЕуDЕФзјБъЮЊ![]()
гжЁпЕуDдкжБЯпy=-2x+1ЩЯЃЌ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]()
ЁрЕуPгыЕуAжиКЯЃЌЕуMгыЕуOжиКЯЃЌ
МДЕуDЕФзјБъЮЊ![]()
злКЯЫљЪіЃЌЕуDЕФзјБъЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]()

 ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ
ПЊаФПьРжМйЦкзївЕЪюМйзївЕЮїАВГіАцЩчЯЕСаД№АИ УћЬтбЕСЗЯЕСаД№АИ
УћЬтбЕСЗЯЕСаД№АИ ЦкФЉМЏНсКХЯЕСаД№АИ
ЦкФЉМЏНсКХЯЕСаД№АИЁОЬтФПЁПСаЗНГЬзщНтгІгУЬтФГаЃзщжЏЁАДѓЪжРаЁЪжЃЌвхТєЯзАЎаФЁБЛюЖЏЃЌМЦЛЎЙКТђКкЁЂАзСНжжбеЩЋЕФЮФЛЏЩРНјааЪжЛцЩшМЦКѓГіЪлЃЌВЂНЋЫљЛёРћШѓШЋВПОшИјЩНЧјРЇФбКЂзгЃЎвбжЊИУбЇаЃДгХњЗЂЪаГЁЛЈ2400дЊЙКТђСЫКкЁЂАзСНжжбеЩЋЕФЮФЛЏЩР100МўЃЌУПМўЮФЛЏЩРЕФХњЗЂМлМАЪжЛцКѓЕФСуЪлМлШчБэЃК
ХњЗЂМлЃЈдЊ) | СуЪлМлЃЈдЊ) | |
КкЩЋЮФЛЏЩР | 25 | 45 |
АзЩЋЮФЛЏЩР | 20 | 35 |
(1)бЇаЃЙКНјКкЁЂАзЮФЛЏЩРИїМИМў?
(2)ЭЈЙ§ЪжЛцЩшМЦКѓШЋВПЪлГіЃЌЧѓИУаЃетДЮвхТєЛюЖЏЫљЛёРћШѓЃЎ











