题目内容
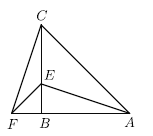
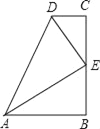
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
取AD的中点F,连接EF.根据平行线的性质可证得(1)(4)(5),根据梯形中位线定理可证得(3)正确.根据全等三角形全等的判定可证得(2)的正误,即可得解.
解:如图:取AD的中点F,连接EF.
∵∠B=∠C=90°,
∴AB∥CD;[结论(5)]
∵E是BC的中点,F是AD的中点,
∴EF∥AB∥CD,2EF=AB+CD(梯形中位线定理)①;
∴∠CDE=∠DEF(两直线平等,内错角相等),
∵DE平分∠ADC,
∴∠CDE=∠FDE=∠DEF,
∴DF=EF;
∵F是AD的中点,∴DF=AF,
∴AF=DF=EF②,
由①得AF+DF=AB+CD,即AD=AB+CD;[结论(3)]
由②得∠FAE=∠FEA,
由AB∥EF可得∠EAB=∠FEA,
∴∠FAE=∠EAB,即EA平分∠DAB;[结论(1)]
由结论(1)和DE平分∠ADC,且DC∥AB,可得∠EDA+∠DAE=90°,则∠DEA=90°,即AE⊥DE;[结论(4)].
由以上结论及三角形全等的判定方法,无法证明△EBA≌△DCE.
正确的结论有4个.
故选:C.

练习册系列答案
相关题目