��Ŀ����
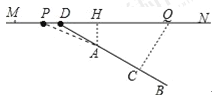
����Ŀ����ͼ��MN��ʾһ�α�ֱ�ĸܵ�·���߶�AB��ʾ�ܵ�·�Ե�һ�ž���¥����֪��A��MN�ľ���Ϊ15�ף�BA���ӳ�����MN�ཻ�ڵ�D������BDN=37�㣬���������ڸ��ٵ�·����ʻʱ����Χ39�����ڻ��ܵ�������Ӱ�죮
��1������A��MN�Ĵ��ߣ�����Ϊ��H������������Ŵ�M��N�ķ�����MN����ʻ�������������P��ʱ��������ʼӰ����һ�ŵľ���¥����ô��ʱ�������H�ľ���Ϊ�����ף�
��2������������һ�ַ������ڸܵ�·��װ�����壬��������ʻ����Qʱ��������һ�ž���¥�ľ���QCΪ39�ף���ô������һ�ž���¥���ܵ�·��װ�ĸ�����������Ҫ�����׳������ο����ݣ�sin37��=0.60��cos37��=0.80��tan37��=0.75��

���𰸡�(1) 36�ף�(2) 81�ף�
��������
�����������1������PA����ֱ����PAH�����ù��ɶ�������PH�ij��ȣ�
��2��������֪��������ij�����PQ�ij��ȣ�ͨ����Rt��ADH��Rt��CDQ�ֱ����DH��DQ�ij��ȣ�Ȼ����ͼ�εõ���PQ=PH+DQ��DH��������߶εij��ȴ�����ֵ���ɣ�
�����������1����ͼ������PA��
������֪��AP=39m��
��ֱ����APH�У�PH=![]() =
=![]() =36���ף���
=36���ף���
�𣺴�ʱ�������H�ľ���Ϊ36�ף�
��2��������֪��������ij�����PQ�ij��ȣ�
��Rt��ADH�У�DH=![]() =20���ף���
=20���ף���
��Rt��CDQ�У�DQ=![]() =65���ף���
=65���ף���
��PQ=PH+HQ=PH+DQ��DH=36+65��20=81���ף���
�𣺸ܵ�·��װ�ĸ�����������Ҫ81�ף�

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�