题目内容
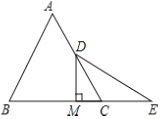
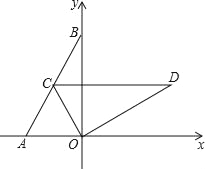
【题目】已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0,![]() ),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
【答案】(1)C(﹣![]() ,
,![]() );(2)
);(2)![]() π+
π+![]() ;(3)
;(3)![]() π﹣
π﹣![]() .
.
【解析】
(1)如图1,过C作CE⊥OA于E,由点A,点B坐标分别为(﹣1,0),(0,),得到OA=1,OB=![]() ,根据旋转的性质得到∠AOC=∠BOD=60°,AO=OC=1,解直角三角形即可得到结论;(2)根据三角形和扇形的面积公式即可得到结论;(3)根据三角形和扇形的面积公式即可得到结论;
,根据旋转的性质得到∠AOC=∠BOD=60°,AO=OC=1,解直角三角形即可得到结论;(2)根据三角形和扇形的面积公式即可得到结论;(3)根据三角形和扇形的面积公式即可得到结论;
(1)如图1,过C作CE⊥OA于E,
∵点A,点B坐标分别为(﹣1,0),(0,![]() ),
),
∴OA=1,OB=![]() ,
,
∵△AOB绕点O顺时针旋转60°得到△COD,
∴∠AOC=∠BOD=60°,AO=OC=1,
∴OE=![]() OC=
OC=![]() ,CE=
,CE=![]() OC=
OC=![]() ,
,
∴C(﹣![]() ,
,![]() );
);
(2)△AOB绕点O顺时针旋转60°所扫过的面积=![]() +
+![]() +
+![]() ×
×![]() =
=![]() π+
π+![]() ;
;
(3)如图2,线段AB绕点O顺时针旋转60°所扫过的面积═(![]() ﹣1×
﹣1×![]() )+(
)+(![]() ﹣
﹣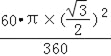 )+(
)+(![]() ﹣
﹣![]() )=
)=![]() π﹣
π﹣![]() .
.

练习册系列答案
相关题目
【题目】股民王先生上周星期五买进某公司股票1000股,每股18元,本周该股票的涨跌情况如表(正数表示价格比前一天上涨,负数表示价格比前一天下跌,单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
(1)星期三结束时,该股票每股多少元?
(2)该股票本周内每股的最高价和最低价分别是多少元?