题目内容
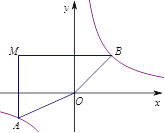
【题目】如图,已知直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.

(1)k的值为 ;当x的取值范围为 时,y1>y2;
(2)若双曲线y2=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.
【答案】(1)8、x>4或﹣4<x<0;(2)15
【解析】
试题分析:(1)根据正比例函数先求出点A的坐标,从而求出了k值为8,然后通过解方程组求得B的坐标,根据图象即可求得y1>y2时的x的取值.;
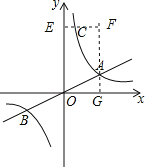
(2)过A、C点分别作x轴、y轴的垂线垂足为G、E,两垂线交于点F,则四边形EFGO是矩形,根据C的纵坐标求得C的坐标,然后根据S△AOC=S矩形﹣SOEC﹣S△CFA﹣S△OAG计算即可.
解:(1)∵点A横坐标为4,
∴由y1=![]() x可知当x=4时,y=2.
x可知当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (k>0)的交点,
(k>0)的交点,
∴k=4×2=8.
∴双曲线的解析式为y=![]() ,
,
解![]() 得
得![]() 或
或![]() ,
,
∴A((4,2),B(﹣4,﹣2),
根据图象可知:当x>4或﹣4<x<0时,y1>y2;
故答案为8、x>4或﹣4<x<0.
(2)如图,过A、C点分别作x轴、y轴的垂线垂足为G、E,两垂线交于点F,则四边形EFGO是矩形,
∵点C在双曲线上,点C的纵坐标为8,
∴8=![]() ,解得x=1,
,解得x=1,
∴C(1,8),
∴S△AOC=S矩形﹣SOEC﹣S△CFA﹣S△OAG=8×4﹣![]() ×1×8﹣
×1×8﹣![]() (4﹣1)×(8﹣2)﹣
(4﹣1)×(8﹣2)﹣![]() ×4×2=32﹣4﹣9﹣4=15.
×4×2=32﹣4﹣9﹣4=15.

练习册系列答案
相关题目