Ő‚ńŅńŕ»›
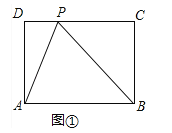
°ĺŐ‚ńŅ°Ņ‘ŕŌ÷ Ķ…ķĽÓ÷–£¨ő“√«ĽŠŅīĶĹ–Ū∂ŗ°įĪÍ◊ľ°ĪĶńĺō–ő£¨»Áő“√«ĶńŅőĪĺ∑‚√ś°ĘA4ĶńīÚ”°÷ĹĶ»£¨∆š Ķ’‚–©ĺō–őĶń≥§”ŽŅŪ÷ģĪ»∂ľő™![]() £ļ1£¨ő“√«≤Ľ∑ŃĺÕį—’‚—ýĶńĺō–ő≥∆ő™°įĪÍ◊ľĺō–ő°Ī£¨‘ŕ°įĪÍ◊ľĺō–ő°ĪABCD÷–£¨Pő™DCĪŖ…Ō“Ľ∂®Ķ„£¨«“CP=BC£¨»ÁÕľňý ĺ£ģ
£ļ1£¨ő“√«≤Ľ∑ŃĺÕį—’‚—ýĶńĺō–ő≥∆ő™°įĪÍ◊ľĺō–ő°Ī£¨‘ŕ°įĪÍ◊ľĺō–ő°ĪABCD÷–£¨Pő™DCĪŖ…Ō“Ľ∂®Ķ„£¨«“CP=BC£¨»ÁÕľňý ĺ£ģ

£®1£©»ÁÕľĘŔ£¨«ů÷§£ļBA=BP£Ľ
£®2£©»ÁÕľĘŕ£¨Ķ„Q‘ŕDC…Ō£¨«“DQ=CP£¨»ŰGő™BCĪŖ…Ō“Ľ∂ĮĶ„£¨ĶĪ°ųAGQĶń÷‹≥§◊Ó–° Ī£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®3£©»ÁÕľĘŘ£¨“—÷™AD=1£¨‘ŕ£®2£©ĶńŐűľĢŌ¬£¨Ń¨Ĺ”AG≤Ę—”≥§ĹĽDCĶń—”≥§ŌŖ”ŕĶ„F£¨Ń¨Ĺ”BF£¨Tő™BFĶń÷–Ķ„£¨M°ĘN∑÷Īūő™ŌŖ∂őPF”ŽAB…ŌĶń∂ĮĶ„£¨«“ ľ÷’Ī£≥÷PM=BN£¨«Ž÷§√ų£ļ°ųMNTĶń√śĽżSő™∂®÷Ķ£¨≤Ę«ů≥Ų’‚łŲ∂®÷Ķ£ģ
°ĺīūįł°Ņ£®1£©÷§√ųľŻĹ‚őŲ£Ľ£®2£©![]() £Ľ£®3£©∂®÷Ķő™£ļ
£Ľ£®3£©∂®÷Ķő™£ļ![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
‘Ő‚∑÷őŲ£ļ£®1£©»ÁÕľĘŔ÷–£¨…ŤAD=BC=a£¨‘ÚAB=CD=![]() a£ģÕ®Ļżľ∆ň„Ķ√≥ŲAB=BP=
a£ģÕ®Ļżľ∆ň„Ķ√≥ŲAB=BP=![]() a£¨”…īňľīŅ…÷§√ų£Ľ
a£¨”…īňľīŅ…÷§√ų£Ľ
£®2£©»ÁÕľĘŕ÷–£¨◊ųQĻō”ŕBCĶń∂‘≥∆Ķ„Q°š£¨Ń¨Ĺ”AQ°šĹĽBC”ŕG£¨īň Ī°ųAQGĶń÷‹≥§◊Ó–°£ģ…ŤAD=BC=QD=a£¨‘ÚAB=CD=![]() a£¨Ņ…Ķ√CQ=CQ°š=
a£¨Ņ…Ķ√CQ=CQ°š=![]() a©Āa£¨”…CQ°š°őAB£¨Õ∆≥Ų
a©Āa£¨”…CQ°š°őAB£¨Õ∆≥Ų![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®3£©»ÁÕľĘŘ÷–£¨◊ųTH°őABĹĽNM”ŕH£¨ĹĽBC”ŕK£ģ”…S°ųMNT=![]() THCK+
THCK+![]() THBK=
THBK=![]() HT£®KC+KB£©=
HT£®KC+KB£©=![]() HTBC=
HTBC=![]() HT£¨ņŻ”√Ő›–őĶń÷–őĽŌŖ∂®ņŪ«ů≥ŲHTľīŅ…Ĺ‚ĺŲő Ő‚£Ľ
HT£¨ņŻ”√Ő›–őĶń÷–őĽŌŖ∂®ņŪ«ů≥ŲHTľīŅ…Ĺ‚ĺŲő Ő‚£Ľ
‘Ő‚Ĺ‚őŲ£ļ£®1£©÷§√ų£ļ»ÁÕľĘŔ÷–£¨…ŤAD=BC=a£¨‘ÚAB=CD=![]() a£ģ
a£ģ
°ŖňńĪŖ–őABCD «ĺō–ő£¨°ŗ°ŌC=90°„£¨°ŖPC=AD=BC=a£¨°ŗPB=![]() =
=![]() a£¨°ŗBA=BP£ģ
a£¨°ŗBA=BP£ģ
£®2£©Ĺ‚£ļ»ÁÕľĘŕ÷–£¨◊ųQĻō”ŕBCĶń∂‘≥∆Ķ„Q°š£¨Ń¨Ĺ”AQ°šĹĽBC”ŕG£¨īň Ī°ųAQGĶń÷‹≥§◊Ó–°£ģ

…ŤAD=BC=QD=a£¨‘ÚAB=CD=![]() a£¨°ŗCQ=CQ°š=
a£¨°ŗCQ=CQ°š=![]() a©Āa£¨°ŖCQ°š°őAB£¨°ŗ
a©Āa£¨°ŖCQ°š°őAB£¨°ŗ![]() =
=![]() =
=![]() =
=![]() £ģ
£ģ
£®3£©÷§√ų£ļ»ÁÕľĘŘ÷–£¨◊ųTH°őABĹĽNM”ŕH£¨ĹĽBC”ŕK£ģ

”…£®2£©Ņ…÷™£¨AD=BC=1£¨AB=CD=![]() £¨DP=CF=
£¨DP=CF=![]() ©Ā1£¨°ŖS°ųMNT=
©Ā1£¨°ŖS°ųMNT=![]() THCK+
THCK+![]() THBK=
THBK=![]() HT£®KC+KB£©=
HT£®KC+KB£©=![]() HTBC=
HTBC=![]() HT£¨°ŖTH°őAB°őFM£¨TF=TB£¨°ŗHM=HN£¨°ŗHT=
HT£¨°ŖTH°őAB°őFM£¨TF=TB£¨°ŗHM=HN£¨°ŗHT=![]() £®FM+BN£©£¨°ŖBN=PM£¨°ŗHT=
£®FM+BN£©£¨°ŖBN=PM£¨°ŗHT=![]() £®FM+PM£©=
£®FM+PM£©=![]() PF=
PF=![]() £®1+
£®1+![]() ©Ā1£©=
©Ā1£©=![]() £¨°ŗS°ųMNT=
£¨°ŗS°ųMNT=![]() HT=
HT=![]() =∂®÷Ķ£ģ
=∂®÷Ķ£ģ

 ŃŃĶ„ľ§ĽÓĺęĪŗŐŠ”Ň100∑÷īů ‘ĺŪŌĶŃ–īūįł
ŃŃĶ„ľ§ĽÓĺęĪŗŐŠ”Ň100∑÷īů ‘ĺŪŌĶŃ–īūįł

