题目内容
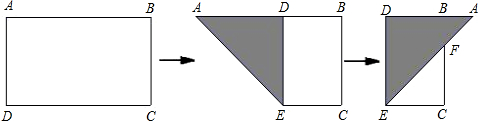
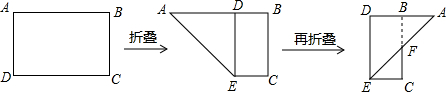
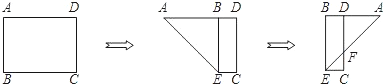
如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB落在AD边上,折痕为AE,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则
的值是( )
| CF |
| CD |

| A、1 | ||
B、
| ||
C、
| ||
D、
|
分析:观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.
解答:解:由题意知:AB=BE=6,BD=AD-AB=2,AD=AB-BD=4;
∵CE∥AB,
∴△ECF∽△ADF,
得
=
=
,
即DF=2CF,所以CF:CD=1:3;
故选C.
∵CE∥AB,
∴△ECF∽△ADF,
得
| CE |
| AD |
| CF |
| DF |
| 1 |
| 2 |
即DF=2CF,所以CF:CD=1:3;
故选C.
点评:此题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,难度不大.

练习册系列答案
相关题目
如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
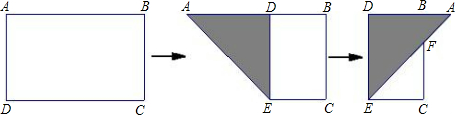

| A、4 | B、6 | C、8 | D、10 |