题目内容
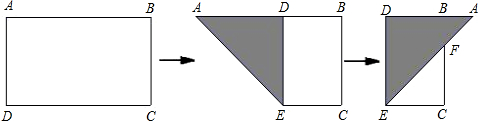
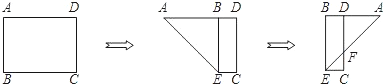
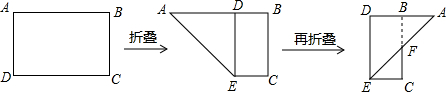
如图，有一矩形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（ ）
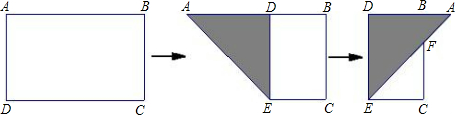
| A、4 | B、6 | C、8 | D、10 |
分析：显然，关键是求CF的长．根据两次折叠后的图形中△ABF∽△ECF得比例线段求解．
解答：解：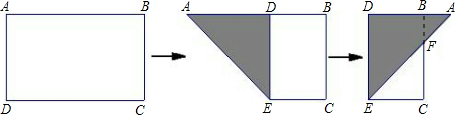
由图可知经过两次折叠后（最右边的图形中），
AB=AD-BD=AD-（10-AD）=2，
BD=EC=10-AD=4．
∵AD∥EC，
∴△AFB∽△EFC．
∴
=
．
∵AB=2，EC=4，
∴FC=2BF．
∵BC=BF+CF=6，
∴CF=4．
S△EFC=EC×CF÷2=8．
故选C．
由图可知经过两次折叠后（最右边的图形中），
AB=AD-BD=AD-（10-AD）=2，
BD=EC=10-AD=4．
∵AD∥EC，
∴△AFB∽△EFC．
∴
| AB |
| EC |
| BF |
| FC |
∵AB=2，EC=4，
∴FC=2BF．
∵BC=BF+CF=6，
∴CF=4．
S△EFC=EC×CF÷2=8．
故选C．
点评：已知折叠问题就是已知图形的全等，然后将所要用到的线段进行适当的转换即可得出结果．
练习册系列答案
名校课堂系列答案
相关题目
