题目内容
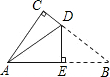如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为
- A.4cm
- B.5cm
- C.6cm
- D.10cm
B
分析：由勾股定理求得AB的长，由题意知BE是AB的一半．
解答：∵两直角边AC=6cm、BC=8cm，
∴AB=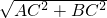
=10cm，
由题意知，点E是AB的中点，故BE=
AB=5cm．
故选B．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，对应边相等．
分析：由勾股定理求得AB的长，由题意知BE是AB的一半．
解答：∵两直角边AC=6cm、BC=8cm，
∴AB=
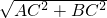=10cm，由题意知，点E是AB的中点，故BE=
AB=5cm．故选B．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，对应边相等．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
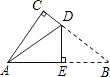如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）| A、4cm | B、5cm | C、6cm | D、10cm |
如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）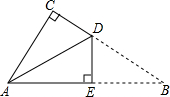
（2012•普陀区一模）如图是一张直角三角形的纸片，直角边AC=6cm，
（2012•香坊区一模）如图是一张直角三角形的纸片．两直角边AC=6cm，BC=8cm将△ABC折叠，使点B与点A重合，折痕为DE，则AD的长为（ ）