题目内容
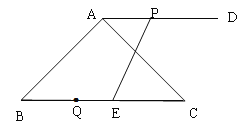
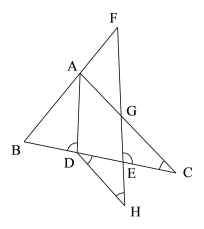
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,AD∥EF.
(1)求证:∠BDA+∠CEG=180°;
(2)若点H在FE的延长线上,且∠F=∠H,则∠EDH与∠C相等吗,请说明理由.
【答案】(1)证明见解析;(2)相等,理由见解析.
【解析】
(1)根据平行线的性质和邻补角的定义结合已知条件分析解答即可;
(2)由AD平分∠BAC结合AD∥EF证得∠F=∠EGC,这样结合∠F=∠H即可得到∠H=∠EGC,由此证得AC∥DH即可得到∠EDG=∠C.
(1)∵AD∥EF,
∴∠BDA=∠BEF,
又∵∠BEF+∠CEG=180°,
∴∠BDA+∠CEG=180°;
(2)∠EDH=∠C,理由如下:
∵AD平分∠BAC交BC于点D,
∴∠BAD=∠CAD,
∵AD∥EF,
∴∠BAD=∠F,∠DAC=∠EGC,
∴∠F=∠EGC,
又∵∠H=∠F,
∴∠H=∠EGC.
∴HD∥AC,
∴∠EDH=∠C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】我们规定:有理数xA用数轴上点A表示,xA叫做点A在数轴上的坐标;有理数xB用数轴上点B表示,xB叫做点B在数轴上的坐标.|AB|表示数轴上的两点A,B之间的距离.
(1)借助数轴,完成下表:
xA | xB | xA﹣xB | |AB| |
3 | 2 | 1 | 1 |
1 | 5 |
|
|
2 | ﹣3 |
|
|
﹣4 | 1 |
|
|
﹣5 | ﹣2 |
|
|
﹣3 | ﹣6 |
|
|
(2)观察(1)中的表格内容,猜想|AB|= ;(用含xA,xB的式子表示,不用说理)
(3)已知点A在数轴上的坐标是﹣2,且|AB|=8,利用(2)中的结论求点B在数轴上的坐标.