题目内容
(2009•赣州二模)如图,在直角坐标系中有一块三角板GEF按图1放置,其中∠GEF=60°,∠G=90°,EF=4.随后三角板的点E沿y轴向点O滑动,同时点F在x轴的正半轴上也随之滑动.当点E到达点O时,停止滑动.(1)在图2中,利用直角三角形外接圆的性质说明点O、E、G、F四点在同一个圆上,并在图2中用尺规方法作出该圆,(不写作法,保留作图痕迹);
(2)滑动过程中直线OG的函数表达式能确定吗?若能,请求出它的表达式;若不能,请说明理由;
(3)求出滑动过程中点G运动的路径的总长;
(4)若将三角板GEF换成一块∠G=90°,∠GEF=α的硬纸板,其它条件不变,试用含α的式子表示点G运动的路径的总长.

【答案】分析:(1)根据∠EOF+∠EGF=180°,可知点O、E、G、F四点在同一个圆上;作出一直角三角形的斜边的中点即为外接圆圆心,斜边的一半为外接圆半径;
(2)设出直线解析式,可求得点G的坐标,代入即可;
(3)画出示意图,利用三角函数可求得滑动路程的和;
(4)方法同(3),只需把度数改为α.
解答: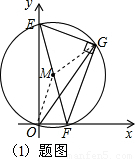 解:(1)取EF的中点M,由直角三角形斜边上的中线等于斜边的一半,知
解:(1)取EF的中点M,由直角三角形斜边上的中线等于斜边的一半,知
ME=MO=MF=MG,
∴O、E、G、F四点在以O为圆心,ME为半径的圆上;
(2)由(1)知∠GOX=∠GEF=60°,
∴滑动过程中∠GOX的度数保持不变,
过图1中的点G作GA⊥x轴,垂足为A,由EF=4,易得GE=2,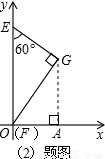
GO=2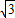 ,在Rt△GOA中可求得G(
,在Rt△GOA中可求得G(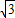 ,3),
,3),
设OG为y=kx,将G(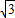 ,3)代入可得k=
,3)代入可得k=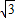 ,
,
∴直线OG的表达式为:y=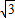 x;
x;
(3)在圆M中,总有OG≤EF=4,
∴滑动过程中OG最长为4,最短为2(此时点E到达点O,停止了滑动),
如图3所示为点G滑动的路径,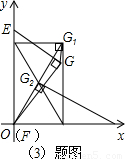
易知GG1=4-2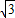 ,G1G2=4-2=2,
,G1G2=4-2=2,
∴点G运动的路径的总长=4-2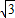 +2=6-2
+2=6-2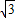 ;
;
(4)当∠GEF=α时,仿上述方法易知∠GOX=α,
且点G的运动路线仅仅是长度上发生了变化,
此时有GG1=4-4sinα,
G1G2=4-4cosα,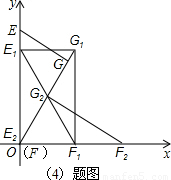
∴点G运动的路径的总长=4-4sinα+4-4cosα
=8-4sinα-4cosα.
点评:直角三角形外接圆的圆心是斜边的中点,外接圆的半径是斜边的一半,注意特殊三角函数的运用,以及类比方法的使用.
(2)设出直线解析式,可求得点G的坐标,代入即可;
(3)画出示意图,利用三角函数可求得滑动路程的和;
(4)方法同(3),只需把度数改为α.
解答:
 解:(1)取EF的中点M,由直角三角形斜边上的中线等于斜边的一半,知
解:(1)取EF的中点M,由直角三角形斜边上的中线等于斜边的一半,知ME=MO=MF=MG,
∴O、E、G、F四点在以O为圆心,ME为半径的圆上;
(2)由(1)知∠GOX=∠GEF=60°,
∴滑动过程中∠GOX的度数保持不变,
过图1中的点G作GA⊥x轴,垂足为A,由EF=4,易得GE=2,

GO=2
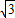 ,在Rt△GOA中可求得G(
,在Rt△GOA中可求得G(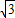 ,3),
,3),设OG为y=kx,将G(
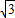 ,3)代入可得k=
,3)代入可得k=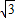 ,
,∴直线OG的表达式为:y=
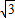 x;
x;(3)在圆M中,总有OG≤EF=4,
∴滑动过程中OG最长为4,最短为2(此时点E到达点O,停止了滑动),
如图3所示为点G滑动的路径,

易知GG1=4-2
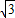 ,G1G2=4-2=2,
,G1G2=4-2=2,∴点G运动的路径的总长=4-2
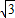 +2=6-2
+2=6-2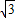 ;
;(4)当∠GEF=α时,仿上述方法易知∠GOX=α,
且点G的运动路线仅仅是长度上发生了变化,
此时有GG1=4-4sinα,
G1G2=4-4cosα,

∴点G运动的路径的总长=4-4sinα+4-4cosα
=8-4sinα-4cosα.
点评:直角三角形外接圆的圆心是斜边的中点,外接圆的半径是斜边的一半,注意特殊三角函数的运用,以及类比方法的使用.

练习册系列答案
相关题目

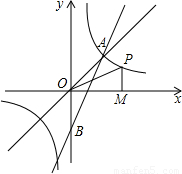
 (k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,已知△POM的面积为2.
(k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,已知△POM的面积为2.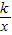 的图象在第一象限内交于点A,求过点A和点B(0,-2)的直线表达式;
的图象在第一象限内交于点A,求过点A和点B(0,-2)的直线表达式;