题目内容
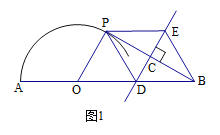
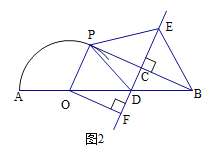
【题目】如图,点O在线段AB上,(不与端点A、B重合),以点O为圆心,OA的长为半径画弧,线段BP与这条弧相切与点P,直线CD垂直平分PB,交PB于点C,交AB于点D,在射线DC上截取DE,使DE=DB。已知AB=6,设OA=r。
(1)求证:OP∥ED;
(2)当∠ABP=30°时,求扇形AOP的面积,并证明四边形PDBE是菱形;
(3)过点O作OF⊥DE于点F,如图所示,线段EF的长度是否随r的变化而变化?若不变,直接写出EF的值;若变化,直接写出EF与r的关系。
【答案】(1)见解析;(2)![]() ,见解析;(3)EF=3
,见解析;(3)EF=3
【解析】试题分析:![]() 根据BP为
根据BP为![]() 的切线,得到
的切线,得到![]() ,
,![]() ,可以推出
,可以推出
![]() ,进而证明平行.
,进而证明平行.
![]() 根据
根据![]() 所对的直角边等于斜边的一半,列出方程,求出半径,根据扇形的面积公式进行即可即可.根据对角线互相垂直平分的四边形是菱形证明.
所对的直角边等于斜边的一半,列出方程,求出半径,根据扇形的面积公式进行即可即可.根据对角线互相垂直平分的四边形是菱形证明.
![]() 根据题意可知,OP∥ED;点
根据题意可知,OP∥ED;点![]() 是
是![]() 的中点,则点
的中点,则点![]() 是
是![]() 的中点,可以用
的中点,可以用![]() 表示出,
表示出,![]() 即可求出
即可求出![]() 的长.
的长.
试题解析:
(1)∵BP为![]() 的切线
的切线
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴OP∥ED;
(2)在Rt△OBP中,![]()
∴![]()
![]()
在Rt△OBP中,![]()
即![]()
解得:![]()
S扇形AOP=![]() ,
,
证明:∵![]()
∴![]()
∵![]()
∴![]() 是等边三角形
是等边三角形![]()
又∵![]()
∴![]()
∴DE与PB互相垂直平分,
∴四边形PDBE是菱形.
(3)线段EF的长度是不会随r的变化而变化,![]()
根据题意可知,OP∥ED;点![]() 是
是![]() 的中点,则点
的中点,则点![]() 是
是![]() 的中点,
的中点,
![]()
![]()
![]()
![]()
![]()
![]()
线段EF的长度是不会随r的变化而变化,![]()

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目