题目内容
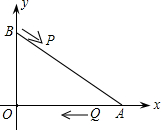 (2012•衡阳)如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<
(2012•衡阳)如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<| 10 | 3 |
(1)当t为何值时,PQ∥BO?
(2)设△AQP的面积为S,
①求S与t之间的函数关系式,并求出S的最大值;
②若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2-x1,y2-y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
分析:(1)如图①所示,当PQ∥BO时,利用平分线分线段成比例定理,列线段比例式
=
,求出t的值;
(2)①求S关系式的要点是求得△AQP的高,如图②所示,过点P作过点P作PD⊥x轴于点D,构造平行线PD∥BO,由线段比例关系
=
求得PD,从而S可求出.S与t之间的函数关系式是一个关于t的二次函数,利用二次函数求极值的方法求出S的最大值;
②本问关键是求出点P、Q的坐标.当S取最大值时,可推出此时PD为△OAB的中位线,从而可求出点P的纵横坐标,又易求Q点坐标,从而求得点P、Q的坐标;求得P、Q的坐标之后,代入“向量PQ”坐标的定义(x2-x1,y2-y1),即可求解.
| AP |
| AB |
| AQ |
| AO |
(2)①求S关系式的要点是求得△AQP的高,如图②所示,过点P作过点P作PD⊥x轴于点D,构造平行线PD∥BO,由线段比例关系
| AP |
| AB |
| PD |
| OB |
②本问关键是求出点P、Q的坐标.当S取最大值时,可推出此时PD为△OAB的中位线,从而可求出点P的纵横坐标,又易求Q点坐标,从而求得点P、Q的坐标;求得P、Q的坐标之后,代入“向量PQ”坐标的定义(x2-x1,y2-y1),即可求解.
解答: 解:(1)∵A、B两点的坐标分别是(8,0)、(0,6),则OB=6,OA=8,
解:(1)∵A、B两点的坐标分别是(8,0)、(0,6),则OB=6,OA=8,
∴AB=
=
=10.
如图①,当PQ∥BO时,AQ=2t,BP=3t,则AP=10-3t.
∵PQ∥BO,
∴
=
,即
=
,
解得t=
,
∴当t=
秒时,PQ∥BO.
(2)由(1)知:OA=8,OB=6,AB=10.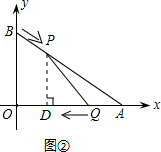
①如图②所示,过点P作PD⊥x轴于点D,则PD∥BO,
∴
=
,即
=
,解得PD=6-
t.
S=
AQ•PD=
•2t•(6-
t)=6t-
t2=-
(t-
)2+5,
∴S与t之间的函数关系式为:S=-
(t-
)2+5(0<t<
),
当t=
秒时,S取得最大值,最大值为5(平方单位).
②如图②所示,当S取最大值时,t=
,
∴PD=6-
t=3,
∴PD=
BO,
又∵PD∥BO,
∴此时PD为△OAB的中位线,则OD=
OA=4,
∴P(4,3).
又∵AQ=2t=
,
∴OQ=OA-AQ=
,∴Q(
,0).
依题意,“向量PQ”的坐标为(
-4,0-3),即(
,-3).
∴当S取最大值时,“向量PQ”的坐标为(
,-3).
 解:(1)∵A、B两点的坐标分别是(8,0)、(0,6),则OB=6,OA=8,
解:(1)∵A、B两点的坐标分别是(8,0)、(0,6),则OB=6,OA=8,∴AB=
| OB2+OA2 |
| 62+82 |
如图①,当PQ∥BO时,AQ=2t,BP=3t,则AP=10-3t.
∵PQ∥BO,
∴
| AP |
| AB |
| AQ |
| AO |
| 10-3t |
| 10 |
| 2t |
| 8 |
解得t=
| 20 |
| 11 |
∴当t=
| 20 |
| 11 |
(2)由(1)知:OA=8,OB=6,AB=10.

①如图②所示,过点P作PD⊥x轴于点D,则PD∥BO,
∴
| AP |
| AB |
| PD |
| OB |
| 10-3t |
| 10 |
| PD |
| 6 |
| 9 |
| 5 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 5 |
| 3 |
∴S与t之间的函数关系式为:S=-
| 9 |
| 5 |
| 5 |
| 3 |
| 10 |
| 3 |
当t=
| 5 |
| 3 |
②如图②所示,当S取最大值时,t=
| 5 |
| 3 |
∴PD=6-
| 9 |
| 5 |
∴PD=
| 1 |
| 2 |
又∵PD∥BO,
∴此时PD为△OAB的中位线,则OD=
| 1 |
| 2 |
∴P(4,3).
又∵AQ=2t=
| 10 |
| 3 |
∴OQ=OA-AQ=
| 14 |
| 3 |
| 14 |
| 3 |
依题意,“向量PQ”的坐标为(
| 14 |
| 3 |
| 2 |
| 3 |
∴当S取最大值时,“向量PQ”的坐标为(
| 2 |
| 3 |
点评:本题是典型的动点型问题,解题过程中,综合利用了平行线分线段成比例定理(或相似三角形的判定与性质)、勾股定理、二次函数求极值及三角形中位线性质等知识点.第(2)②问中,给出了“向量PQ”的坐标的新定义,为题目增添了新意,不过同学们无须为此迷惑,求解过程依然是利用自己所熟悉的数学知识.

练习册系列答案
相关题目
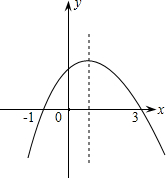 (2012•衡阳)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
(2012•衡阳)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法: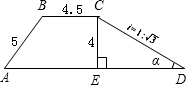 (2012•衡阳)如图,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD.(i=CE:ED,单位:m)
(2012•衡阳)如图,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD.(i=CE:ED,单位:m)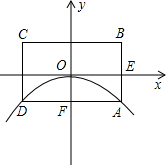 (2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)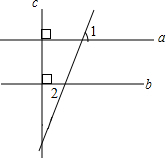 (2012•衡阳)如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
(2012•衡阳)如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )