��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��l1��y��kx+b��k��bΪ��������k��0������A��B���㣬��A��y���ϣ�
��1����B����������1��2����
��b���� �����ú�����ĸk�Ĵ���ʽ��ʾ��
������OAB�����Ϊ2ʱ����ֱ��l1�ı���ʽ��
��2����B������Ϊ��k��2b��b��b2������C����1��s��Ҳ��ֱ��l1�ϣ�
����s��ֵ��
�����ֱ��l1��y��kx+b��k��0����ֱ��l2��y��x���ڵ㣨x1��y1������0��x1��2����k��ȡֵ��Χ��
���𰸡���1����2+k����y��2x+4����2����0����![]() ��
��
��������
(1)�ٰ�B(��1��2)����y=kx+b�������b��ֵ��
�ڸ��������ε�����������k��ֵ���Ӷ��ɵ�ֱ�߽���ʽ��
(2)�ٰѵ�B�͵�C���뺯������ʽ�������s��ֵ��
�ڸ�������ֱ�ߵĽ�������ĺ������ȡֵ��Χ�������k��ȡֵ��Χ��
(1)����B(��1��2)����y=kx+b��
��b=2+k��
�ʴ�Ϊ��2+k��
����S��OAB=![]() (2+k)��1=2
(2+k)��1=2
��ã�k=2��
����ֱ��l1�ı���ʽΪ��y=2x+4��
(2)����ֱ��l1��y=kx+b������B(k��2b��b��b2)�͵�C(��1��s)��
��k(k��2b)+b=b��b2����k+b=s
�����ã�(b��k)2=0��
����s=b��k=0��
����ֱ��l1��y=kx+b(k��0)��ֱ��l2��y=x���ڵ�(x1��y1)��
��kx1+b=x1
(1��k)x1=b��
��b��k=0��
��b=k��
��x1=![]()
��0��x1��2��
��![]() ��0��
��0��![]() ��2
��2
��ã�![]() ��
��
��k��ȡֵ��Χ��![]() ��
��

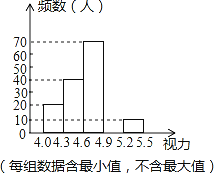
����Ŀ��ijУΪ�˽���꼶ѧ����������������꼶��ѧ��������һ���������飬�����������ݽ���ͳ�����������Ƴ�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��һ���֣�
���� | Ƶ�����ˣ� | Ƶ�� |
4.0��x��4.3 | 20 | 0.1 |
4.3��x��4.6 | 40 | 0.2 |
4.6��x��4.9 | 70 | 0.35 |
4.9��x��5.2 | a | 0.3 |
5.2��x��5.5 | 10 | b |
��1����Ƶ���ֲ����У�a=�� ����b=�� ����
��2����Ƶ���ֲ�ֱ��ͼ����������
��3����������4.6���ϣ���4.6����������������������������ռ�����������İٷֱ��Ƕ��٣�