题目内容
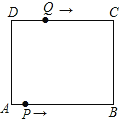
【题目】如图在长方形ABCD中,AB=12cm,BC=8cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,用x(秒)表示运动时间.
(1)求点P和点Q相遇时的x值.
(2)连接PQ,当PQ平分矩形ABCD的面积时,求运动时间x值.
(3)若点P、点Q运动到6秒时同时改变速度,点P的速度变为每秒3cm,点Q的速度为每秒1cm,求在整个运动过程中,点P、点Q在运动路线上相距路程为20cm时运动时间x值.


【答案】(1)x=![]() ;(2)4 或20;(3)4或14.5
;(2)4 或20;(3)4或14.5
【解析】
试题(1)根据P、Q两点运动的路程和等于AB+BC+CD列方程求解即可;
(2)分点P在AB边上,点Q在CD边上和点Q运动到A点,点P运动到点C两种情况进行讨论即可得;
(3)分变速前与变速后两种情况进行即可得.
试题解析:(1)由题意得:x+2x=12×2+8,解得: x=![]() ;
;
(2)当点P在AB边上,点Q在CD边上,由题意得:2x=12-x 解得,x=4 ;
当点Q运动到点A时,用时(12+8+12)÷2=16秒,此时点P运动到BC边上,当点P运动到点C时,PQ平分矩形ABCD的面积,此时用时:(12+8)÷1=20 秒,
综上:当PQ平分矩形ABCD在面积时,x的值为4或20;
(3)变速前:x+2x=32-20,解得:x=4 ;
变速后:12+(x-6)+6+3×(x-6)=32+20,解得:x=14.5;
综上:x的值为4或14.5.

练习册系列答案
相关题目