Question

【题目】已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．

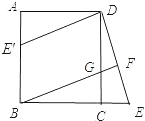
（1）求证：△BCG≌△DCE；

（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。

Answer 1

【答案】（1）答案见解析；（2）答案见解析

【解析】试题分析：（1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）．

（2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形．

（1）证明：∵四边形ABCD是正方形，

∴BC=CD，∠BCD=90°．

∵∠BCD+∠DCE=180°，

∴∠BCD=∠DCE=90°．

又∵CG=CE，

∴△BCG≌△DCE．

（2）解：四边形E′BGD是平行四边形．理由如下：

∵△DCE绕D顺时针旋转90°得到△DAE′，

∴CE=AE′．

∵CE=CG，

∴CG=AE′．

∵四边形ABCD是正方形，

∴BE′∥DG，AB=CD．

∴AB﹣AE′=CD﹣CG．

即BE′=DG．

∴四边形E′BGD是平行四边形．