题目内容
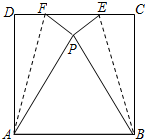 如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是
如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是分析:过P作PH⊥DC于H,交AB于G,由正方形的性质得到AD=AB=BC=DC=2;∠D=∠C=90°;再根据折叠的性质有PA=PB=2,∠FPA=∠EPB=90°,可判断△PAB为等边三角形,利用等边三角形的性质得到∠APB=60°,PG=
AB=
,于是∠EPF=120°,PH=HG-PG=2-
,得∠HEP=30°,然后根据含30°的直角三角形三边可求出HE,得到EF,最后利用三角形的面积公式计算即可.
| ||
| 2 |
| 3 |
| 3 |
解答: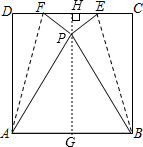 解:过P作PH⊥DC于H,交AB于G,如图,
解:过P作PH⊥DC于H,交AB于G,如图,
则PG⊥AB,
∵四边形ABCD为正方形,
∴AD=AB=BC=DC=2;∠D=∠C=90°,
又∵将正方形ABCD折叠,使点C与点D重合于形内点P处,
∴PA=PB=2,∠FPA=∠EPB=90°,
∴△PAB为等边三角形,
∴∠APB=60°,PG=
AB=
,
∴∠EPF=120°,PH=HG-PG=2-
,
∴∠HEP=30°,
∴HE=
PH=
(2-
)=2
-3,
∴EF=2HE=4
-6,
∴△EPF的面积=
FE•PH=
(2-
)(4
-6)
=7
-12.
故答案为7
-12.
 解:过P作PH⊥DC于H,交AB于G,如图,
解:过P作PH⊥DC于H,交AB于G,如图,则PG⊥AB,
∵四边形ABCD为正方形,
∴AD=AB=BC=DC=2;∠D=∠C=90°,
又∵将正方形ABCD折叠,使点C与点D重合于形内点P处,
∴PA=PB=2,∠FPA=∠EPB=90°,
∴△PAB为等边三角形,
∴∠APB=60°,PG=
| ||
| 2 |
| 3 |
∴∠EPF=120°,PH=HG-PG=2-
| 3 |
∴∠HEP=30°,
∴HE=
| 3 |
| 3 |
| 3 |
| 3 |
∴EF=2HE=4
| 3 |
∴△EPF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
=7
| 3 |
故答案为7
| 3 |
点评:本题考查了折叠的性质:折叠前后的两图形全等,即对应角相等,对应线段相等.也考查了正方形和等边三角形的性质以及含30°的直角三角形三边的关系.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
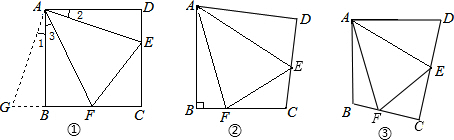
 如图,将正方形纸片按图甲中的虚线对折得到图乙,再对折得到图丙,在图丙中沿虚线将△ABC(AB≠BC)剪下,再将△ABC展开铺平所得图形是( )
如图,将正方形纸片按图甲中的虚线对折得到图乙,再对折得到图丙,在图丙中沿虚线将△ABC(AB≠BC)剪下,再将△ABC展开铺平所得图形是( ) (1)如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7:
(1)如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7: 0°)绕点B按顺时针转动一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,那么这个角度等于
0°)绕点B按顺时针转动一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,那么这个角度等于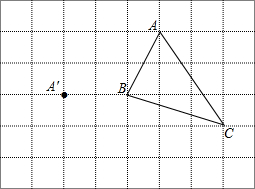 如图,将三角形ABC进行平移,使点A的对应点为点A′
如图,将三角形ABC进行平移,使点A的对应点为点A′ ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想. ∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).