题目内容
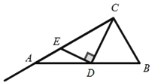
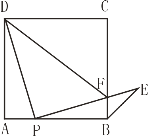
【题目】如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF.
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当![]() 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.
【答案】(1)证明见解析(2)45°(3)见解析
【解析】
(1)根据∠ADP与∠EPB都是∠APD的余角,根据同角的余角相等,即可求证;
(2)首先证得△PAD≌△EQP,可以证得△BEQ是等腰直角三角形,可以证得∠EBQ=45°,即可证得∠CBE=45°;
(3)这两个三角形是直角三角形,若相似,则对应边的比相等,即可求得![]() 的值.
的值.
(1)证明:∵四边形ABCD是正方形.
∴∠A=∠PBC=90°,AB=AD,
∴∠ADP+∠APD=90°,
∵∠DPE=90°,
∴∠APD+∠EPB=90°,
∴∠ADP=∠EPB;
(2)解:过点E作EQ⊥AB交AB的延长线于点Q,则∠EQP=∠A=90°,

又∵∠ADP=∠EPB,PD=PE,
∴△PAD≌△EQP,
∴EQ=AP,AD=AB=PQ,
∴AP=EQ=BQ,
∴∠CBE=∠EBQ=45°;
(3)![]() .
.
理由:∵△PFD∽△BFP,
∴![]() ,
,
∵∠ADP=∠EPB,∠CBP=∠A
∴△DAP∽△PBF
∴![]() ,
,
∴PA=PB
∴当![]() 时,△PFD∽△BFP.
时,△PFD∽△BFP.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目