题目内容
 (2007•西城区二模)若等边△ABC的边长为6cm长,内切圆O分别切三边于D、E、F,则阴影部分的面积是( )
(2007•西城区二模)若等边△ABC的边长为6cm长,内切圆O分别切三边于D、E、F,则阴影部分的面积是( )分析:连接OA,OE,OF,OD,AD,则AD过O,求出BD、AD,求出三角形ABC的面积,根据S△OBC=
S△ABC,求出OD,求出∠BOC,根据扇形的面积公式求出即可.
| 1 |
| 3 |
解答:解:连接OA,OE,OF,OD,AD,则AD过O,
∵AB=AC,AD⊥BC,
∴BD=DC=3,
由勾股定理得:AD=
=
=3
,
∴S△ABC=
BC×AD=
×6×3
=9
,
∵等边三角形ABC的内切圆⊙O分别且AB、BC、AC于F、D、E,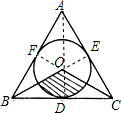
∴OF⊥AB,OD⊥BC,OE⊥AC,
∵AB=BC=AC=6,OD=OE=OF,
∴S△AOC=S△OBC=S△OAC,
∴S△OBC=
S△ABC=3
,
∴
BC×OD=3
,
即
×6OD=3
,
∴OD=
,
∵⊙O是等边△ABC的内切圆,
∴∠OBC=
∠ABC=30°,
同理∠OCB=30°,
∴∠BOC=180°-30°-30°=120°,
∴阴影部分的面积是:
=π,
故选A.
∵AB=AC,AD⊥BC,
∴BD=DC=3,
由勾股定理得:AD=
| AB2-BD2 |
| 62-32 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵等边三角形ABC的内切圆⊙O分别且AB、BC、AC于F、D、E,

∴OF⊥AB,OD⊥BC,OE⊥AC,
∵AB=BC=AC=6,OD=OE=OF,
∴S△AOC=S△OBC=S△OAC,
∴S△OBC=
| 1 |
| 3 |
| 3 |
∴
| 1 |
| 2 |
| 3 |
即
| 1 |
| 2 |
| 3 |
∴OD=
| 3 |
∵⊙O是等边△ABC的内切圆,
∴∠OBC=
| 1 |
| 2 |
同理∠OCB=30°,
∴∠BOC=180°-30°-30°=120°,
∴阴影部分的面积是:
120π×
| ||||
| 360 |
故选A.
点评:本题考查了扇形的面积,三角形的面积,勾股定理,三角形的内切圆,等边三角形性质等知识点的应用,关键是求出OD的长和∠BOC的度数,主要考查学生综合运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
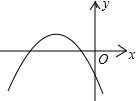 (2007•西城区二模)已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
(2007•西城区二模)已知二次函数y=ax2+bx+c的图象如图所示,下列结论: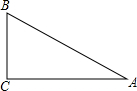 (2007•西城区二模)如图,在Rt△ABC中,斜边AB=8,∠B=60°,将△ABC绕点B旋转60°,顶点C运动的路线长是( )
(2007•西城区二模)如图,在Rt△ABC中,斜边AB=8,∠B=60°,将△ABC绕点B旋转60°,顶点C运动的路线长是( )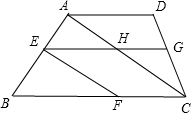 (2007•西城区二模)如图,已知AD∥EG∥BC,且AC∥EF,记∠EFB=α,则图中等于α的角(不包含∠EFB)的个数为( )
(2007•西城区二模)如图,已知AD∥EG∥BC,且AC∥EF,记∠EFB=α,则图中等于α的角(不包含∠EFB)的个数为( )