Question

【题目】如图，已知在△ABC中 AB = AC，点 D为 BC边的中点，点 F在边 AB上，点E在 线段 DF的延长线上，且∠BAE =∠BDF，点 M在线段 DF上，且∠EBM =∠C．

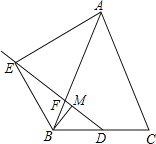
（1）求证： EB BD BM AB ；

（2）求证：AE⊥BE．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据等腰三角形的性质得到∠ABC=∠C，由已知条件得到∠EBM=∠C，等量代换得到∠EBM=∠ABC，求得∠ABE=∠DBM，推出△BEA∽△BDM，根据相似三角形的性质得到，于是得到结论；
（2）连接AD，由等腰三角形的性质得到AD⊥BC，推出△ABD∽△EBM，根据相似三角形的性质得到∠ADB=∠EMB=90°，求得∠AEB=∠BMD=90°，于是得到结论．

（1）∵ ∴．

∵ ∴．

∴，

即：．

又∵．

∴．

∴

（2）连结．

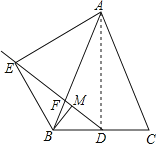
∵，点为边的中点，

∴，

∴．

∵，

∴．

又∵，

∴．

∴，

∴．

又∵，

∴．

∴．