题目内容
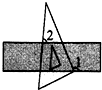 如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是
如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是
- A.95°
- B.85°
- C.75°
- D.65°
B
分析:根据题画出图形,由直尺的两对边AB与CD平行,利用两直线平行,同位角相等可得∠1=∠3,由∠1的度数得出∠3的度数,又∠3为三角形EFG的外角,根据外角性质:三角形的外角等于与它不相邻的两内角之和得到∠3=∠E+∠2,把∠3和∠E的度数代入即可求出∠2的度数.
解答: 已知:AB∥CD,∠1=115°,∠E=30°,
已知:AB∥CD,∠1=115°,∠E=30°,
求:∠2的度数?
解:∵AB∥CD(已知),且∠1=115°,
∴∠3=∠1=115°(两直线平行,同位角相等),
又∠3为△EFG的外角,且∠E=30°,
∴∠3=∠2+∠E,
则∠2=∠3-∠E=115°-30°=85°.
故选B.
点评:此题考查了平行线的性质,以及三角形的外角性质,利用了转化的数学思想,其中平行线的性质有:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,熟练掌握性质是解本题的关键.
分析:根据题画出图形,由直尺的两对边AB与CD平行,利用两直线平行,同位角相等可得∠1=∠3,由∠1的度数得出∠3的度数,又∠3为三角形EFG的外角,根据外角性质:三角形的外角等于与它不相邻的两内角之和得到∠3=∠E+∠2,把∠3和∠E的度数代入即可求出∠2的度数.
解答:
 已知:AB∥CD,∠1=115°,∠E=30°,
已知:AB∥CD,∠1=115°,∠E=30°,求:∠2的度数?
解:∵AB∥CD(已知),且∠1=115°,
∴∠3=∠1=115°(两直线平行,同位角相等),
又∠3为△EFG的外角,且∠E=30°,
∴∠3=∠2+∠E,
则∠2=∠3-∠E=115°-30°=85°.
故选B.
点评:此题考查了平行线的性质,以及三角形的外角性质,利用了转化的数学思想,其中平行线的性质有:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,熟练掌握性质是解本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
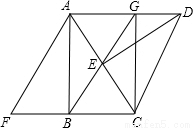
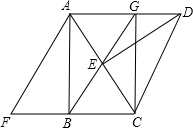 如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.
如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE. 如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是( )
如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是( )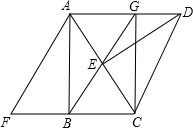 如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.
如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.