题目内容
 如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.
如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.(1)求证:四边形ADCE是菱形.
(2)连接BF并延长交AE于G,连接CG.请问:四边形ABCG是什么特殊平行四边形?为什么?
分析:(1)需证明△ACD是等边三角形、△AFC是等边三角形,即可证明四边形AFCD是菱形;
(2)可先证四边形ABCG是平行四边形,再由∠ABC=90°,可证四边形ABCG是矩形.
(2)可先证四边形ABCG是平行四边形,再由∠ABC=90°,可证四边形ABCG是矩形.
解答:证明:(1)∵三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,
∴△ABC≌△ABF,且∠BAC=∠BAF=30°,
∴∠FAC=60°,
∴AD=DC=AC,
又∵△ABC≌△EFC,
∴CA=CE,
又∵∠ECF=60°,
∴AC=EC=AE,
∴AD=DC=CE=AE,
∴四边形ADCE是菱形;

(2)
证明:由(1)可知:△ACD,△AFC是等边三角形,△ACB≌△AFB,
∴∠EDC=∠BAC=
∠FAC=30°,且△ABC为直角三角形,
∴BC=
AC,
∵EC=CB,
∴EC=
AC,
∴E为AC中点,
∴DE⊥AC,
∴AE=EC,
∵AG∥BC,
∴∠EAG=∠ECB,∠AGE=∠EBC,
∴△AEG≌△CEB,
∴AG=BC,(7分)
∴四边形ABCG是平行四边形,
∵∠ABC=90°,
∴四边形ABCG是矩形.
∴△ABC≌△ABF,且∠BAC=∠BAF=30°,
∴∠FAC=60°,
∴AD=DC=AC,
又∵△ABC≌△EFC,
∴CA=CE,
又∵∠ECF=60°,
∴AC=EC=AE,
∴AD=DC=CE=AE,
∴四边形ADCE是菱形;

(2)
证明:由(1)可知:△ACD,△AFC是等边三角形,△ACB≌△AFB,
∴∠EDC=∠BAC=
| 1 |
| 2 |
∴BC=
| 1 |
| 2 |
∵EC=CB,
∴EC=
| 1 |
| 2 |
∴E为AC中点,
∴DE⊥AC,
∴AE=EC,
∵AG∥BC,
∴∠EAG=∠ECB,∠AGE=∠EBC,
∴△AEG≌△CEB,
∴AG=BC,(7分)
∴四边形ABCG是平行四边形,
∵∠ABC=90°,
∴四边形ABCG是矩形.
点评:此题主要考查菱形和矩形的判定,综合应用等边三角形的判定、全等三角形的判定等知识是解题的关键.

练习册系列答案
相关题目
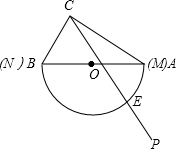 为O),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.
为O),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E. (2012•南平模拟)如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且
(2012•南平模拟)如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且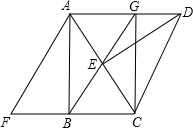 如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.
如图,在一个含30°的三角板ABC中,将三角板沿着AB所在直线翻转180°得到△ABF,再将三角板绕点C顺时针方向旋转60°得到△DEC,点F在AC上,连接AE.