题目内容
(1)请大家阅读下面两段材料,并解答问题:
材料1:我们知道在数轴上表示3和1的两点之间的距离为2(如图1),而|3-1|=2,所以在数轴上表示3和1的两点之间的距离
为|3-1|.
(2)再如在数轴上表示4和-2的两点之间的距离为6(如图2)而|4-(-2)|=6,所以数轴上表示数4和-2的两点之间的距离
为|4-(-2)|.
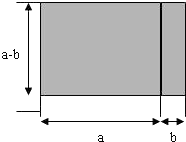
(3)根据上述规律,我们可以得出结论:在数轴上表示数a和数b两点之间的距离等于
(4)试一试,求在数轴上表示的数5
与-4
的两点之间的距离为
(5)已知数轴上表示数a的点M与表示数-1的点之间的距离为3,表示数b的点N与表示数2的点之间的距离为4,求M,N两点之间的距离.

材料1:我们知道在数轴上表示3和1的两点之间的距离为2(如图1),而|3-1|=2,所以在数轴上表示3和1的两点之间的距离
为|3-1|.
(2)再如在数轴上表示4和-2的两点之间的距离为6(如图2)而|4-(-2)|=6,所以数轴上表示数4和-2的两点之间的距离
为|4-(-2)|.
(3)根据上述规律,我们可以得出结论:在数轴上表示数a和数b两点之间的距离等于
|a-b|
|a-b|
(如图3)(4)试一试,求在数轴上表示的数5
| 2 |
| 3 |
| 1 |
| 4 |
9
| 11 |
| 12 |
9
.| 11 |
| 12 |
(5)已知数轴上表示数a的点M与表示数-1的点之间的距离为3,表示数b的点N与表示数2的点之间的距离为4,求M,N两点之间的距离.

分析:(3)(4)根据数轴上两点间的距离=两个数之差的绝对值,算出即可;
(5)先分别得到表示数a的点M与表示数,表示数b的点N,再根据两点间的距离公式求出即可.
(5)先分别得到表示数a的点M与表示数,表示数b的点N,再根据两点间的距离公式求出即可.
解答:解:(3)在数轴上表示数a和数b两点之间的距离等于|a-b|;
(4)在数轴上表示的数5
与-4
的两点之间的距离为:|5
-(-4
)|=9
;
(5)数轴上表示数a的点M为-4或2;表示数b的点N为-2或6;
当点M为-4,点N为-2时,M,N两点之间的距离为|-4-(-2)|=2;
当点M为-4,点N为6时,M,N两点之间的距离为|-4-6|=10;
当点M为2,点N为-2时,M,N两点之间的距离为|2-(-2)|=4;
当点M为2,点N为6时,M,N两点之间的距离为|6-2|=4.
故M,N两点之间的距离为2或4或10.
故答案为:|a-b|;9
.
(4)在数轴上表示的数5
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 11 |
| 12 |
(5)数轴上表示数a的点M为-4或2;表示数b的点N为-2或6;
当点M为-4,点N为-2时,M,N两点之间的距离为|-4-(-2)|=2;
当点M为-4,点N为6时,M,N两点之间的距离为|-4-6|=10;
当点M为2,点N为-2时,M,N两点之间的距离为|2-(-2)|=4;
当点M为2,点N为6时,M,N两点之间的距离为|6-2|=4.
故M,N两点之间的距离为2或4或10.
故答案为:|a-b|;9
| 11 |
| 12 |
点评:本题主要考查了数轴和绝对值,掌握数轴上两点间的距离=两个数之差的绝对值.

练习册系列答案
相关题目
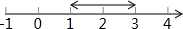

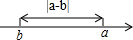
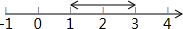
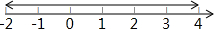
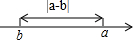
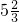 与
与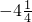 的两点之间的距离为______;
的两点之间的距离为______;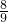 )2-(49
)2-(49 )2=______;
)2=______;

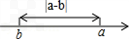
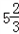 与
与 的两点之间的距离为( );
的两点之间的距离为( ); )2﹣(49
)2﹣(49 )2=( );
)2=( );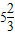 与
与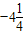 的两点之间的距离为______.
的两点之间的距离为______.