题目内容
若两组数x1,x2,…,xn和y1,y2,…yn,它们的平均数分别为. |
| x |
. |
| y |
分析:平均数的计算方法是求出所有数据的和,然后除以数据的总个数.
解答:解:由题意知,
(x1+x2+…xn)=
,
(y1+y2+…yn)=
新的一组数x1+y1,x2+y2,…,xn+yn的平均数=
(x1+y1+x2+y2+…+xn+yn)
=
(x1+x2+…xn)+
(y1+y2+…yn)=
+
.
故答案为
+
.
| 1 |
| n |
. |
| x |
| 1 |
| n |
. |
| y |
新的一组数x1+y1,x2+y2,…,xn+yn的平均数=
| 1 |
| n |
=
| 1 |
| n |
| 1 |
| n |
. |
| x |
. |
| y |
故答案为
. |
| x |
. |
| y |
点评:本题考查了平均数的概念.记住本题的结论.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 和
和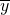 ,那么新的一组数x1+y1,x2+y2,…,xn+yn的平均数是________.
,那么新的一组数x1+y1,x2+y2,…,xn+yn的平均数是________.