题目内容
若两组数x1,x2,…,xn和y1,y2,…yn,它们的平均数分别为
和
,那么新的一组数x1+y1,x2+y2,…,xn+yn的平均数是______.
| . |
| x |
| . |
| y |
由题意知,
(x1+x2+…xn)=
,
(y1+y2+…yn)=
新的一组数x1+y1,x2+y2,…,xn+yn的平均数=
(x1+y1+x2+y2+…+xn+yn)
=
(x1+x2+…xn)+
(y1+y2+…yn)=
+
.
故答案为
+
.
| 1 |
| n |
| . |
| x |
| 1 |
| n |
| . |
| y |
新的一组数x1+y1,x2+y2,…,xn+yn的平均数=
| 1 |
| n |
=
| 1 |
| n |
| 1 |
| n |
| . |
| x |
| . |
| y |
故答案为
| . |
| x |
| . |
| y |

练习册系列答案
相关题目
 和
和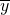 ,那么新的一组数x1+y1,x2+y2,…,xn+yn的平均数是________.
,那么新的一组数x1+y1,x2+y2,…,xn+yn的平均数是________.