Question

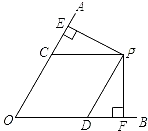
如图，点P是∠AOB的平分线上的一点，作PD⊥OA，垂足为D，PE⊥OB垂足为E，DE交OC于点F．则在图中：
（1）总共有______对全等三角形；
（2）总共______个直角．

Answer 1

（1）有三对全等三角形．由“AAS”可知△ODP≌△OEP，又由“SAS”可知：△ODF≌△OEF，△PDF≌△PEF．
（2）共有八个直角，由（1）中的△ODF≌△OEF可知：∠OFD=∠OFE，而∠OFD+∠OFE=180°，因此OF⊥ED．这样以F为顶点有四个直角，另有已知的四个直角，共计八个直角．
故分别填3，8．
分析：根据已知并利用全等三角形的判定方法可以求得有三对全等三角形，有八个直角．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．