题目内容
如图，点P是∠AOB内的一点，过点P作PC∥OB，PD∥OA，分别交OA、OB于点C、D，且PE⊥OA，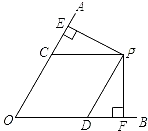
PF⊥OB，垂足分别为点E、F．（1）求证：OC•CE=OD•DF；
（2）当点P位于∠AOB的什么位置时，四边形CODP是菱形并证明你的结论．
分析：（1）欲证OC•CE=OD•DF，可证△PCE∽△PDF；
（2）通过一组邻边相等的平行四边形是菱形（菱形定义）可知点P在∠AOB的位置．
（2）通过一组邻边相等的平行四边形是菱形（菱形定义）可知点P在∠AOB的位置．
解答：（本题共2小题，第（1）小题（5分），第（2）小题（5分），满分10分）
证明：（1）∵PC∥OB，PD∥OA，
∴四边形OCPD是平行四边形，且∠ECP=∠O，∠FDP=∠O．（1分）
∴PC=OD，PD=OC，∠ECP=∠FDP．（1分）
∵PE⊥OA，PF⊥OB，
∴∠PEC=∠PFD=90°．
∴△PCE∽△PDF．（1分）
∴
=
．
即得
=
．（1分）
∴OC•CE=OD•DF．（1分）
（2）当点P在∠AOB的平分线上时，四边形CODP是菱形．（1分）
∵当点P在∠AOB的平分线上时，由PE⊥OA，PF⊥OB，得PE=PF，
∴由△PCE∽△PDF，得
=
=1，即得PC=PD．（2分）
∵四边形CODP是平行四边形，
∴四边形CODP是菱形．（1分）
当点P不在∠AOB的平分线上时，可得PE≠PF．即得PC≠PD．
∴当点P不在∠AOB的平分线上时，四边形CODP不是菱形．（1分）
证明：（1）∵PC∥OB，PD∥OA，
∴四边形OCPD是平行四边形，且∠ECP=∠O，∠FDP=∠O．（1分）
∴PC=OD，PD=OC，∠ECP=∠FDP．（1分）
∵PE⊥OA，PF⊥OB，
∴∠PEC=∠PFD=90°．
∴△PCE∽△PDF．（1分）
∴
| CE |
| DF |
| PC |
| PD |
即得
| CE |
| DF |
| OD |
| OC |
∴OC•CE=OD•DF．（1分）
（2）当点P在∠AOB的平分线上时，四边形CODP是菱形．（1分）
∵当点P在∠AOB的平分线上时，由PE⊥OA，PF⊥OB，得PE=PF，
∴由△PCE∽△PDF，得
| PE |
| PF |
| PC |
| PD |
∵四边形CODP是平行四边形，
∴四边形CODP是菱形．（1分）
当点P不在∠AOB的平分线上时，可得PE≠PF．即得PC≠PD．
∴当点P不在∠AOB的平分线上时，四边形CODP不是菱形．（1分）
点评：乘积的形式通常可以转化为比例的形式，本题考查相似三角形的判定和性质及菱形判定的理解及运用．
练习册系列答案
相关题目
63、如图，点P是∠AOB的平分线上的一点，作PD⊥OA，垂足为D，PE⊥OB垂足为E，DE交OC于点F．则在图中：
24、如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．
如图，点P是∠AOB内部一点，点P关于OA、OB的对称点是H、G，直线HG交OA、OB于点C、D，若HG=4cm，且∠AOB=30°，则△HOG的周长是