ΧβΡΩΡΎ»ί
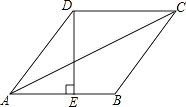
ΓΨΧβΡΩΓΩ»γΆΦΘ§¥”Ήσ±ΏΒΎ“ΜΗωΗώΉ”ΩΣ Φœρ”“ ΐΘ§‘ΎΟΩΗω–ΓΗώΉ”÷–ΕΦΧν»κ“ΜΗω’ϊ ΐΘ§ ΙΒΟΤδ÷–»Έ“β»ΐΗωœύΝΎΗώΉ”÷–ΥυΧν’ϊ ΐ÷°ΚΆΕΦœύΒ»Θ°
Θ®![]() Θ©Ω…«σΒΟ
Θ©Ω…«σΒΟ![]() __________Θ§ΒΎ
__________Θ§ΒΎ![]() ΗωΗώΉ”÷–ΒΡ ΐΈΣ__________Θ°
ΗωΗώΉ”÷–ΒΡ ΐΈΣ__________Θ°
Θ®![]() Θ©≈–ΕœΘΚ«Α
Θ©≈–ΕœΘΚ«Α![]() ΗωΗώΉ”÷–ΥυΧν’ϊ ΐ÷°ΚΆ «ΖώΩ…ΡήΈΣ
ΗωΗώΉ”÷–ΥυΧν’ϊ ΐ÷°ΚΆ «ΖώΩ…ΡήΈΣ![]() ΘΩ»τΡήΘ§«σ≥ω
ΘΩ»τΡήΘ§«σ≥ω![]() ΒΡ÷ΒΘ§»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘ§»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
Θ®![]() Θ©»τ»Γ«Α
Θ©»τ»Γ«Α![]() ΗώΉ”÷–ΒΡ»Έ“βΝΫΗω ΐΦ«Ής
ΗώΉ”÷–ΒΡ»Έ“βΝΫΗω ΐΦ«Ής![]() ΓΔ
ΓΔ![]() Θ§«“
Θ§«“![]() Θ§Ρ«Ο¥Υυ”–ΒΡ
Θ§Ρ«Ο¥Υυ”–ΒΡ![]() ΒΡΚΆΩ…“‘Ά®ΙΐΦΤΥψ
ΒΡΚΆΩ…“‘Ά®ΙΐΦΤΥψ![]() ΒΟΒΫΘ§ΤδΫαΙϊΈΣ__________ΘΜ»τ
ΒΟΒΫΘ§ΤδΫαΙϊΈΣ__________ΘΜ»τ![]() ΓΔ
ΓΔ![]() ΈΣ«Α
ΈΣ«Α![]() ΗώΉ”÷–ΒΡ»Έ“βΝΫΗω ΐΦ«Ής
ΗώΉ”÷–ΒΡ»Έ“βΝΫΗω ΐΦ«Ής![]() ΓΔ
ΓΔ![]() Θ§«“
Θ§«“![]() Θ§‘ρΥυ”–ΒΡ
Θ§‘ρΥυ”–ΒΡ![]() ΒΡΚΆΈΣ__________Θ°
ΒΡΚΆΈΣ__________Θ°
ΓΨ¥πΑΗΓΩΘ®![]() Θ©
Θ©![]() ΘΜ
ΘΜ ![]() Θ®
Θ®![]() Θ©ΡήΘ§
Θ©ΡήΘ§ ![]() Θ®
Θ®![]() Θ©
Θ©![]()
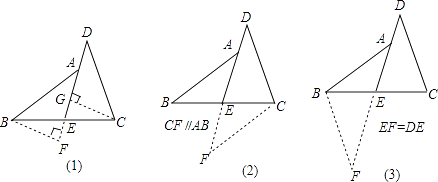
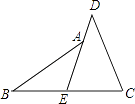
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨί»ΐΗωœύΝΎΗώΉ”ΒΡ’ϊ ΐΒΡΚΆœύΒ»Ν– Ϋ«σ≥ωxΒΡ÷ΒΘ§‘ΌΗυΨίΒΎ9Ηω ΐ «2Ω…ΒΟΓν=2Θ§»ΜΚσ’“≥ωΗώΉ”÷–ΒΡ ΐ «ΟΩ3ΗωΈΣ“ΜΗω―≠ΜΖΉι“ά¥Έ―≠ΜΖΘ§‘Ό”Ο2017≥ΐ“‘3Θ§ΗυΨί”ύ ΐΒΡ«ιΩω»ΖΕ®”κΒΎΦΗΗω ΐœύΆ§Φ¥Ω…ΒΟΫβΘΜ
Θ®2Θ©Ω…œ»ΦΤΥψ≥ω’β»ΐΗω ΐΒΡΚΆΘ§‘ΌΑ¥’’Ιφ¬…ΦΤΥψΘ°
Θ®3Θ©”…”Ύ «»ΐΗω ΐ÷ΊΗ¥≥ωœ÷Θ§“ρ¥ΥΩ…”Ο«Α»ΐΗω ΐΒΡ÷ΊΗ¥Εύ¥ΈΦΤΥψ≥ωΫαΙϊΘ°
‘ΧβΫβΈωΘΚΫβΘΚΘ®![]() Θ©ΓΏ»Έ“β»ΐΗωœύΝΎΗώΉ”÷–ΥυΧνΒΡ’ϊ ΐ÷°ΚΆΕΦœύΒ»Θ§Γύ±μΗώ÷–¥”Ήσœρ”“»ΐΗω ΐΉ÷“ΜΗω―≠ΜΖΘ§Γύ
Θ©ΓΏ»Έ“β»ΐΗωœύΝΎΗώΉ”÷–ΥυΧνΒΡ’ϊ ΐ÷°ΚΆΕΦœύΒ»Θ§Γύ±μΗώ÷–¥”Ήσœρ”“»ΐΗω ΐΉ÷“ΜΗω―≠ΜΖΘ§Γύ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§Γύ
Θ§Γύ![]() Θ§ΓύΒΎ
Θ§ΓύΒΎ![]() ΗωΗώΉ”÷–ΧνΒΡ ΐ «
ΗωΗώΉ”÷–ΧνΒΡ ΐ «![]() Θ°
Θ°
Θ®![]() Θ©ΡήΘ§
Θ©ΡήΘ§ ![]() Θ°ΓΏ
Θ°ΓΏ![]() ΘΜ
ΘΜ ![]() ΘΜ”Ο
ΘΜ”Ο![]() Θ°
Θ°
Β±«Α![]() ΗωΗώΉ”÷–ΒΡ ΐΒΡΚΆ «
ΗωΗώΉ”÷–ΒΡ ΐΒΡΚΆ «![]() Θ§ΓύΕύ“ΜΗωΗώΉ” ΐΒΡΚΆ «
Θ§ΓύΕύ“ΜΗωΗώΉ” ΐΒΡΚΆ «![]() Θ§‘ΌΕύ“ΜΗωΗώΉ”ΒΡ ΐΒΡΚΆ «
Θ§‘ΌΕύ“ΜΗωΗώΉ”ΒΡ ΐΒΡΚΆ «![]() ΖϊΚœΧβ“βΘ§Υυ“‘
ΖϊΚœΧβ“βΘ§Υυ“‘![]() ΒΡ÷Β «
ΒΡ÷Β «![]() Θ°
Θ°
Θ®![]() Θ©ΓΏ»Γ«Α
Θ©ΓΏ»Γ«Α![]() ΗώΉ”÷–ΒΡ»Έ“βΝΫΗω ΐΘ§Φ«Ής
ΗώΉ”÷–ΒΡ»Έ“βΝΫΗω ΐΘ§Φ«Ής![]() Θ§
Θ§ ![]() Θ§«“
Θ§«“![]() Θ§ΓύΥυ”–
Θ§ΓύΥυ”–![]() ΒΡΚΆΈΣΘΚ
ΒΡΚΆΈΣΘΚ ![]() Θ°ΓΏ”…”Ύ»ΐΗω ΐ÷ΊΗ¥≥ωœ÷Θ§Ρ«Ο¥«Α
Θ°ΓΏ”…”Ύ»ΐΗω ΐ÷ΊΗ¥≥ωœ÷Θ§Ρ«Ο¥«Α![]() ΗώΉ”÷–’β»ΐΗω ΐ
ΗώΉ”÷–’β»ΐΗω ΐ![]() ≥ωœ÷ΝΥ
≥ωœ÷ΝΥ![]() ¥ΈΘ§
¥ΈΘ§ ![]() ΚΆ
ΚΆ![]() Ης≥ωœ÷ΝΥ
Ης≥ωœ÷ΝΥ![]() ¥ΈΘ§Γύ¥ζ»κ ΫΉ”Ω…ΒΟ
¥ΈΘ§Γύ¥ζ»κ ΫΉ”Ω…ΒΟ![]() Θ§
Θ§
¥πΘΚ ![]() ΫαΙϊΈΣ
ΫαΙϊΈΣ![]() Θ§Υυ”–ΒΡ
Θ§Υυ”–ΒΡ![]() ΒΡΚΆΈΣ
ΒΡΚΆΈΣ![]() Θ°
Θ°

 ”ά«§ΫΧ”ΐΚ°ΦΌΉς“ΒΩλά÷ΦΌΤΎ―”±Ώ»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ
”ά«§ΫΧ”ΐΚ°ΦΌΉς“ΒΩλά÷ΦΌΤΎ―”±Ώ»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ