Question

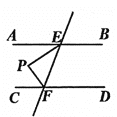
【题目】如图，直线AB//CD，直线EF交AB于点E，交CD于点F，EP平分∠AEF，FP平分∠CFE，∠BEP＝α，∠DFP＝β，则a＋β＝( )

A.180°B.225°C.270°D.315°

Answer 1

【答案】C

【解析】

根据平行线的性质，由AB∥CD得到∠AEF+∠CFE=180°，再根据角平分线定义得∠PEF+∠PFE=(∠AEF+∠CFE)，然后计算出∠EPF=90°，再由∠BEP+∠EPF+∠PFD=360°，即可求出a＋β的值.

解：∵AB∥CD，

∴∠AEF+∠CFE=180°，

又∵EP平分∠AEF，FP平分∠EFC

∴∠PEF+∠PFE=(∠AEF+∠CFE)=×180°=90°

∴∠EPF=90°

又∠BEF+∠EFD=180°，且△PEF内角和为360°

∴∠BEP+∠EPF+∠PFD=360°

∴∠BEP+∠PFD＝α+β=360°-∠EPF=360°-90°=270°.

故选：C