题目内容
在△ABC中,以AD为直径的圆与△ABC的边BC相切于点D,交AB、AC于点E、F.(1)说明:∠BAC+∠EDF=180°;
(2)若BD=CD,探索:∠EDF与∠C之间有何数量关系?说明你的理由.
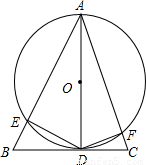
【答案】分析:(1)根据AD为直径,∠AED=∠AFD=90°,再由四边形内角和定理证明∠BAC+∠EDF=180°;
(2)由于⊙O与BC相切于D点,AD为直径,可证AD⊥BC,而BD=CD,则AD为BC边的中垂线,可证△ABC为等腰三角形,得∠B=∠C,再根据三角形内角和定理及(1)的结论探索关系.
解答:(1)证明:∵AD为直径,∴∠AED=∠AFD=90°,
在四边形AEDF中,∵∠AED+∠AFD+∠BAC+∠EDF=360°,
∴∠BAC+∠EDF=180°;
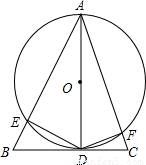
(2)解:∠EDF=2∠C.
理由:∵⊙O与BC相切于D点,AD为直径,
∴AD⊥BC,
又∵BD=CD,∴AD为BC边的中垂线,
∴AB=AC,∴∠B=∠C,
∵在△ABC中,∠BAC+∠B+∠C=180°,而∠BAC+∠EDF=180°,
∴∠EDF=∠B+∠C=2∠C.
点评:本题考查了切线的性质,圆周角定理.关键是由圆周角定理证明直角,由切线的性质证明垂直关系.
(2)由于⊙O与BC相切于D点,AD为直径,可证AD⊥BC,而BD=CD,则AD为BC边的中垂线,可证△ABC为等腰三角形,得∠B=∠C,再根据三角形内角和定理及(1)的结论探索关系.
解答:(1)证明:∵AD为直径,∴∠AED=∠AFD=90°,
在四边形AEDF中,∵∠AED+∠AFD+∠BAC+∠EDF=360°,
∴∠BAC+∠EDF=180°;

(2)解:∠EDF=2∠C.
理由:∵⊙O与BC相切于D点,AD为直径,
∴AD⊥BC,
又∵BD=CD,∴AD为BC边的中垂线,
∴AB=AC,∴∠B=∠C,
∵在△ABC中,∠BAC+∠B+∠C=180°,而∠BAC+∠EDF=180°,
∴∠EDF=∠B+∠C=2∠C.
点评:本题考查了切线的性质,圆周角定理.关键是由圆周角定理证明直角,由切线的性质证明垂直关系.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 (2013•龙岗区模拟)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(2013•龙岗区模拟)如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. 已知:如图,在△ABC中,以AB为直径的⊙O交BC于点D,交CA的延长线于点E.
已知:如图,在△ABC中,以AB为直径的⊙O交BC于点D,交CA的延长线于点E.
 在△ABC中,以AD为直径的圆与△ABC的边BC相切于点D,交AB、AC于点E、F.
在△ABC中,以AD为直径的圆与△ABC的边BC相切于点D,交AB、AC于点E、F.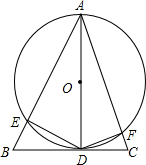 在△ABC中,以AD为直径的圆与△ABC的边BC相切于点D,交AB、AC于点E、F.
在△ABC中,以AD为直径的圆与△ABC的边BC相切于点D,交AB、AC于点E、F.