题目内容
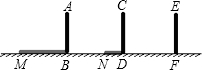电线杆上有一盏路灯O，电线杆与三个等高的标杆整齐划一地排列在马路的一侧，AB、CD、EF是三个标杆，相邻的两个标杆之间的距离都是2m，已知AB、CD在灯光下的影长分别为BM=1.6m，DN=0.6m．则标杆EF的影长为（ ）| A、1.2 | B、0.8 | C、0.4 | D、0.2 |
分析：解此题要借助于相似三角形的性质，相似三角形的对应边成比例，还要注意数形结合思想与方程思想的应用．
解答：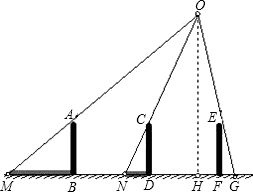
解：作射线MA、NC，设它们相交于点O，连接OE并延长交MF于点G．过O作OH⊥MG于点H，设DH=x．
由AB∥CD∥OH，得
=
，
即
=
，
解得x=1.2m．
设FG=y，同理得
=
，
即
=
，
解得y=0.4．
所以EF的影长为0.4m．
故选：C．
解：作射线MA、NC，设它们相交于点O，连接OE并延长交MF于点G．过O作OH⊥MG于点H，设DH=x．由AB∥CD∥OH，得
| MB |
| MH |
| ND |
| NH |
即
| 1.6 |
| 3.6+X |
| 0.6 |
| 0.6+X |
解得x=1.2m．
设FG=y，同理得
| FG |
| HG |
| ND |
| NH |
即
| y |
| 0.8+y |
| 0.6 |
| 1.8 |
解得y=0.4．
所以EF的影长为0.4m．
故选：C．
点评：此题主要考查的是相似三角形的应用，把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求解即可，体现了方程的思想．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
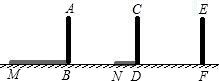的一侧，AB、CD、EF是三个标杆，相邻的两个标杆之间的距离都是2 m，已知AB、CD在灯光下的影长分别为BM=1.6 m，DN=0.6m．
