题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?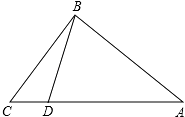
【答案】解:∵∠ABC=90°,AB=4,BC=3,
∴AC= ![]() =5,
=5,
分三种情况:
①CD=BD时,∠C=∠DBC,
∵∠C+∠A=∠DBC+∠DBA=90°,
∴∠A=∠DBA,
∴BD=AD,
∴CD=AD= ![]() AC=2.5,即t=2.5;
AC=2.5,即t=2.5;
②当CD=BC时,CD=3,即t=3;
③当BD=BC时,过点B作BF⊥AC于F,如图所示: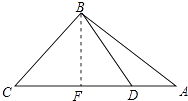
则CF=DF,△ABC的面积= ![]() ABBC=
ABBC= ![]() ACBF,
ACBF,
∴BF= ![]() =2.4,
=2.4,
∴CF= ![]() =
= ![]() =1.8,
=1.8,
∴CD=3.6,即t=3.6.
综上所述:当运动时间t为2.5或3或3.6秒时,以点C、B、D为顶点的三角形是等腰三角形.
【解析】根据已知条件,利用勾股定理求出AC的长,要判断以点C、B、D为顶点的三角形是等腰三角形,分三种情况讨论:①CD=BD时,∠C=∠DBC,②当CD=BC时③当BD=BC时,分别求出运动时间t的值即可。

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目