题目内容
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
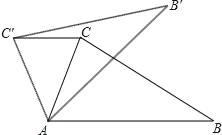
A. 30° B. 35° C. 40° D. 50°
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
题目内容
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )

A. 30° B. 35° C. 40° D. 50°
 备战中考寒假系列答案
备战中考寒假系列答案